题目内容
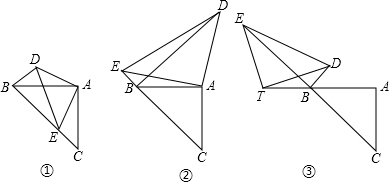
11. 如图,⊙O的半径为10,点M是AO延长线上的动点,⊙M和⊙O内切于点A,点C是⊙O上一点,连结AC交⊙M于点B,cos∠CAM=$\frac{3}{5}$,连结CM,设MO=x.
如图,⊙O的半径为10,点M是AO延长线上的动点,⊙M和⊙O内切于点A,点C是⊙O上一点,连结AC交⊙M于点B,cos∠CAM=$\frac{3}{5}$,连结CM,设MO=x.(1)设BC=y,求y关于x的函数解析式及定义域;
(2)当△BCM是等腰三角形时,求x的值;
(3)设CM与⊙O交于点D,当点C恰好是弧$\widehat{AD}$的中点时,求⊙M的半径.
分析 (1)先利用直径所对的圆周角是直角,得出FC∥EB,进而得出,△ACF∽△ABE,即$\frac{AC}{AB}=\frac{AF}{AE}$,代值即可得出结论;
(2)分三种情况计算,①当BM=CM时,判断出点C与点A重合,不符合题意,②当BC=BM时,建立方程$\frac{6}{5}$x=x+10求解即可,③当BC=CM时,建立方程),$\frac{\frac{1}{2}(x+10)}{\frac{6}{5}x}=\frac{3}{5}$,求解即可;
(3)先由$\widehat{AC}=\widehat{CD}$得出,∠AOC=∠DOC,进而判断出,∠ABM=∠CMB,即可得出CM=CB,求出圆M的半径.
解答 解:(1)如图1,
连接CF,BE,在⊙O中,AF是直径,
∴∠ACF=90°,
在Rt△ACF中,cos∠CAM=$\frac{3}{5}$,AF=20,
∴AC=12,CF=16,
∵AE是⊙M的直径,
∴∠ABE=90°,
∴FC∥EB,
∴△ACF∽△ABE,
∴$\frac{AC}{AB}=\frac{AF}{AE}$,
∵AB=y+12,AF=20,AC=12,AE=2x+20,
∴$\frac{12}{y+12}=\frac{20}{2x+20}$,
∴y=$\frac{6}{5}$x(x>0);
(2)∵△BCM是等腰三角形,
∴①当BM=CM时.
∵BM是⊙M的半径,
∴点C在⊙M上,
即:点C与点A重合,不符合题意;
②当BC=BM时,BC=AM=x+10,
∵BC=y=$\frac{6}{5}$x,
∴$\frac{6}{5}$x=x+10,
∴x=50;
③当BC=CM时,如图2,
过点C作CG⊥BM,
∴BG=$\frac{1}{2}$BM=$\frac{1}{2}$(x+10),
∵AM=BM,
∴∠CAM=∠ABM,
在Rt△BCG中,cos∠ABM=$\frac{BG}{BC}$=$\frac{3}{5}$,
∵BC=y=$\frac{6}{5}$x,BG=$\frac{1}{2}$(x+10),
∴$\frac{\frac{1}{2}(x+10)}{\frac{6}{5}x}=\frac{3}{5}$,
∴x=$\frac{250}{11}$;
即:x的值为50或$\frac{250}{11}$;
(3)如图3, 连接OD,OC,
连接OD,OC,
当点C恰好是$\widehat{AD}$的中点时,
∴∠AOC=∠DOC,
∴∠OCA=∠OCD,
∴∠DCA=2∠OCA,
∵∠OCA=∠ABM,
∴∠DCA=∠2∠ABM,
∴∠ABM=∠CMB,
∴CM=CB,
由(2)③知,x=OM=$\frac{250}{11}$,
∴AM=MO+OA=$\frac{250}{11}$+10=$\frac{360}{11}$
即⊙M的半径为$\frac{360}{11}$.
点评 此题是圆的综合题,主要考查了圆的性质,直径所对的圆周角是直角,等腰三角形的性质和判定,相似三角形的性质和判定,解本题的关键是分类讨论,用方程的思想求解.

| A. | 216 | B. | 217 | C. | 218 | D. | 219 |




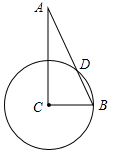 如图,在Rt△ABC中,∠ACB=90°,AB=2BC,以C为圆心,以CB为半径的圆交AB于点D,求$\widehat{BD}$的度数.
如图,在Rt△ABC中,∠ACB=90°,AB=2BC,以C为圆心,以CB为半径的圆交AB于点D,求$\widehat{BD}$的度数.