题目内容
(本小题满分9分)
如图,在平面直角坐标系中,矩形OCDE的三个顶点分别是C(3,0),D(3,4),E(0,4).点A在DE上,以A为顶点的抛物线过点C,且对称轴x=1交x轴于点B.连接EC,AC.点P,Q为动点,设运动时间为t秒.
(1)直接写出点A坐标,并求出该抛物线的解析式.
(2)在图1中,若点P在线段OC上从点O向点C以1个单位/秒的速度运动,同时点Q在线段CE上从点C向点E以2个单位/秒的速度运动,当一个点到达终点时,另一个点随之停止运动.当t为何值时,△PCQ为直角三角形?
(3)在图2中,若点P在对称轴上从点B开始向点A以2个单位/秒的速度运动,过点P作PF⊥AB,交AC于点F,过点F作FG⊥AD于点G,交抛物线于点Q,连接AQ,CQ.当t为何值时,△ACQ的面积最大?最大值是多少?

练习册系列答案
相关题目
14.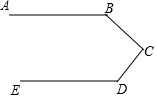 如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=130°,∠D=120°,则∠C的度数为( )
如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=130°,∠D=120°,则∠C的度数为( )
 如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=130°,∠D=120°,则∠C的度数为( )
如图,是赛车跑道的一段示意图,其中AB∥DE,测得∠B=130°,∠D=120°,则∠C的度数为( )| A. | 120° | B. | 110° | C. | 140° | D. | 90° |
12. 如右图,AB∥CD,直线l分别交AB、CD于E、F,∠1=56°,则∠2的度数是( )
如右图,AB∥CD,直线l分别交AB、CD于E、F,∠1=56°,则∠2的度数是( )
 如右图,AB∥CD,直线l分别交AB、CD于E、F,∠1=56°,则∠2的度数是( )
如右图,AB∥CD,直线l分别交AB、CD于E、F,∠1=56°,则∠2的度数是( )| A. | 56° | B. | 146° | C. | 134° | D. | 124° |



 B.
B.  C.
C.  D. 7
D. 7 的方程
的方程 的解是________.
的解是________. 的解为( )
的解为( ) B.
B.  C.
C.  D.
D. 

