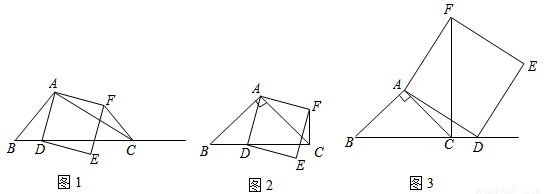
如图.是赛车跑道的一段示意图.其中AB∥DE.测得∠B=130°.∠D=120°.则∠C的度数为( )A．120°B．110°C．140°D．90° 题目和参考答案——青夏教育精英家教网—

题目内容

14．

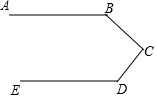如图，是赛车跑道的一段示意图，其中AB∥DE，测得∠B=130°，∠D=120°，则∠C的度数为（　　）

A．

120°

B．

110°

C．

140°

D．

90°

分析过点C作CF∥AB，由平行线性质可得∠B，∠D，∠BCF，∠DCF的关系，进而求得∠C．

解答解：如图所示：过点C作CF∥AB．

∵AB∥DE，
∴DE∥CF；
∴∠BCF=180°-∠B=50°，∠DCF=180°-∠D=60°；
∴∠C=∠BCF+∠DCF=110°．
故选：B．

点评本题主要考查了两直线平行，同旁内角互补的性质，解题时需要作辅助线求解．

练习册系列答案

相关题目

在△ABC中，∠ACB为锐角，点D为射线BC上一点，连接AD，以AD为一边且在AD的右侧作正方形ADEF．如果AB=AC，∠BAC=90o，

（1）当点D在线段BC上时（与点B不重合），如图2，线段CF 、BD所在直线的位

置关系为 __________，线段CF 、BD的数量关系为；

（2）当点D在线段BC的延长线上时，如图3，①中的结论是否仍然成立，并说明理由．

(本小题满分9分)

如图，在平面直角坐标系中，矩形OCDE的三个顶点分别是C(3，0)，D(3，4)，E(0，4)．点A在DE上，以A为顶点的抛物线过点C，且对称轴x＝1交x轴于点B．连接EC，AC．点P，Q为动点，设运动时间为t秒．

（1）直接写出点A坐标，并求出该抛物线的解析式．

（2）在图1中，若点P在线段OC上从点O向点C以1个单位/秒的速度运动，同时点Q在线段CE上从点C向点E以2个单位/秒的速度运动，当一个点到达终点时，另一个点随之停止运动．当t为何值时，△PCQ为直角三角形？

（3）在图2中，若点P在对称轴上从点B开始向点A以2个单位/秒的速度运动，过点P作PF⊥AB，交AC于点F，过点F作FG⊥AD于点G，交抛物线于点Q，连接AQ，CQ．当t为何值时，△ACQ的面积最大？最大值是多少？

3．一只蚂蚁沿着数轴从表示$\frac{1}{5}$的点爬到表示$\frac{4}{5}$的点，它经过的表示分数的点有（　　）

10．

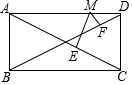如图，在矩形ABCD中，AB=5，AD=12，M是AD上异于A和D的任意一点，且ME⊥AC于E，MF⊥BD于F，则ME+MF为（　　）

18．

如图，已知AB∥CD，∠A=70°，则∠1的补角的度数是（　　）

5．简便计算．
（1）489²-487×491；
（2）$\frac{1}{4}$×6.16²-6.16×2.08+4×1.04²．

20．已知平面直角坐标系内的一点P（2，-3），则点P到x轴的距离是（　　）

1．在平面直角坐标系中，把直线y=2x向左平移1个单位长度，平移后的直线解析式是y=2x+2．

试题分类