题目内容
 两个反比例函数y=
两个反比例函数y= ,y=
,y= 在第一象限内的图象如图所示,点P1,P2,P3,…,P2010在反比例函数y=
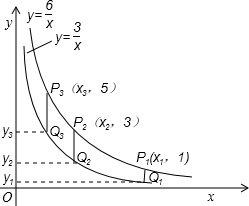
在第一象限内的图象如图所示,点P1,P2,P3,…,P2010在反比例函数y= 图象上,它们的横坐标分别是x1,x2,x3,…,x2010,纵坐标分别是1,3,5,…,共2010个连续奇数,过点P1,P2,P3,…,P2010分别作y轴的平行线,与y=
图象上,它们的横坐标分别是x1,x2,x3,…,x2010,纵坐标分别是1,3,5,…,共2010个连续奇数,过点P1,P2,P3,…,P2010分别作y轴的平行线,与y= 的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2010(x2010,y2010),则y2010=
的图象交点依次是Q1(x1,y1),Q2(x2,y2),Q3(x3,y3),…,Q2010(x2010,y2010),则y2010=
- A.2010
- B.4020
- C.2009.5
- D.2008.5
C
分析:因为点P1,P2,P3,…,P2010在反比例函数y= 图象上,根据P1,P2,P3的纵坐标,推出P2010的纵坐标,再根据y=
图象上,根据P1,P2,P3的纵坐标,推出P2010的纵坐标,再根据y= 和y=
和y= 的关系,求出y2010的值.
的关系,求出y2010的值.
解答:∵P1,P2,P3的纵坐标为1,3,5,是连续奇数,
∴Pn的纵坐标为:2n-1;
∴P2010的纵坐标为2×2010-1=4019.
∵y= 与y=
与y= 在横坐标相同时,y=
在横坐标相同时,y= 的纵坐标是y=
的纵坐标是y= 的纵坐标的2倍,
的纵坐标的2倍,
∴y2010= ×4019=2009.5.
×4019=2009.5.
故选C.
点评:本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式.
分析:因为点P1,P2,P3,…,P2010在反比例函数y=
 图象上,根据P1,P2,P3的纵坐标,推出P2010的纵坐标,再根据y=
图象上,根据P1,P2,P3的纵坐标,推出P2010的纵坐标,再根据y= 和y=
和y= 的关系,求出y2010的值.
的关系,求出y2010的值.解答:∵P1,P2,P3的纵坐标为1,3,5,是连续奇数,
∴Pn的纵坐标为:2n-1;
∴P2010的纵坐标为2×2010-1=4019.
∵y=
 与y=
与y= 在横坐标相同时,y=
在横坐标相同时,y= 的纵坐标是y=
的纵坐标是y= 的纵坐标的2倍,
的纵坐标的2倍,∴y2010=
 ×4019=2009.5.
×4019=2009.5.故选C.
点评:本题考查的是反比例函数图象上点的坐标特点,即反比例函数图象上各点的坐标一定适合此函数的解析式.

练习册系列答案
 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案
相关题目
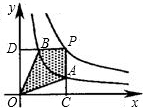 ,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( )
,PC⊥x轴于点C,交C2于点A,PD⊥y轴于点D,交C2于点B,下列说法正确的是( ) 如图,两个反比例函数
如图,两个反比例函数
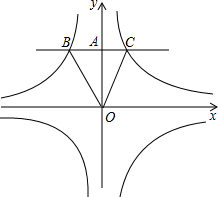 如图,已知反比例函数y=
如图,已知反比例函数y= 已知两个反比例函数
已知两个反比例函数