题目内容
在△ABC中，∠BAC=90°，AD⊥BC，DF⊥AB，EF⊥BC．求证：BD：BC=BE：BD．考点：相似三角形的判定与性质
专题：证明题
分析：由EF∥AD可得
=
，由DF∥AC可得
=
，可得出结论．
| BE |
| BD |
| BF |
| BA |
| BF |
| BA |
| BD |
| BC |
解答：证明：
∵AD⊥BC，EF⊥BC，
∴EF∥AD，
∴
=
，
∵∠BAC=90°，DF⊥AB，
∴DF∥AC，
∴
=
，
∴BD：BC=BE：BD．
∵AD⊥BC，EF⊥BC，
∴EF∥AD，
∴
| BE |
| BD |
| BF |
| BA |
∵∠BAC=90°，DF⊥AB，
∴DF∥AC，
∴
| BF |
| BA |
| BD |
| BC |
∴BD：BC=BE：BD．
点评：本题主要考查平行线分线段成比例的性质，掌握平行线分线段中的线段对应成比例是解题的关键．
练习册系列答案
相关题目
如图所示，在△ABC中，AC＞AB，点D在AC上（不与A、C重合），
如图，直线AB，CD相交于点O，OC是∠AOE的平分线，∠BOD与∠COE相等吗？为什么？
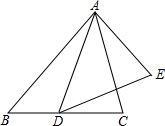如图，