题目内容
20.解不等式组$\left\{\begin{array}{l}3(x+1)>x+5\\ \frac{x-1}{2}≤\frac{x}{3}\end{array}\right.$(要求:画出数轴并根据数轴写不等式的解集)分析 先求出每个不等式的解集,再求出不等式组的解集即可.
解答 解:$\left\{\begin{array}{l}{3(x+1)>x+5①}\\{\frac{x-1}{2}≤\frac{x}{3}②}\end{array}\right.$
∵解不等式①得:x>1,
解不等式②得:x≤2,
在数轴上表示为:
∴不等式组的解集为1<x≤2.
点评 本题考查了解一元一次不等式组和再数轴上表示不等式的解集,能根据不等式的解集求出不等式组的解集是解此题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.下面式子从左边到右边的变形是因式分解的是( )
| A. | x2-x-2=x(x-1)-2 | B. | x2-4x+4=(x-2)2 | C. | (x+1)(x-1)=x2-1 | D. | x-1=x(1-$\frac{1}{x}$) |
5.下列多项式乘法中,可用平方差公式计算的是( )
| A. | (2a+b)(2a-3b) | B. | (x-2y)(x+2y) | C. | (x+1)(1+x) | D. | (-x-y)(x+y) |
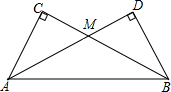 把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,MC=4cm,则点M到直线AB的距离为4cm.
把两个同样大小的含30°角的三角尺像如图所示那样放置,其中M是AD与BC的交点,MC=4cm,则点M到直线AB的距离为4cm.