题目内容
11.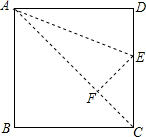 如图,将正方形纸片ABCD折叠两次,第一次折痕为AC,第二次折痕为AE,且点D落在点F处.若正方形边长是1,求DE的长.
如图,将正方形纸片ABCD折叠两次,第一次折痕为AC,第二次折痕为AE,且点D落在点F处.若正方形边长是1,求DE的长.
分析 首先由勾股定理可求得AC=$\sqrt{2}$的长,然后由翻折的性质可求得AF=1,从而可求得FC=$\sqrt{2}$-1,接下来证明△EFC为等腰直角三角形,可求得FE=$\sqrt{2}$-1,最后根据翻折的性质可求得DE=$\sqrt{2}$-1.
解答 解:由勾股定理得:AC=$\sqrt{A{B}^{2}+B{C}^{2}}$=$\sqrt{2}$.
由翻折的性质可知:DE=EF,AD=AF=1,∠D=∠EFA=90°.
则FC=AC-AF=$\sqrt{2}$-1.
由正方形的性质可知:∠ECF=45°.
∴∠FEC=180°-45°-90°=45°.
∴∠FEC=∠ECF.
∴EF=FC=$\sqrt{2}$-1.
∴DE=$\sqrt{2}$-1.
点评 本题主要考查的是翻折的性质、勾股定理的应用、等腰直角三角形的判定,证得△EFC为等腰直角三角形是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
2.小刚想利用下列长度的木棒摆成一个三角形,下列各组你认为可行的是( )
| A. | 5,2,2 | B. | 2,3,6 | C. | 2,3,4 | D. | 7,13,6 |
19.单项式-23a2b3的系数和次数分別是( )
| A. | -2,8 | B. | -8,5 | C. | 2,8 | D. | -2,5 |
16.计算(-3)2的结果为( )
| A. | 9 | B. | 6 | C. | -9 | D. | -6 |
 -3x=x2-5x+1
-3x=x2-5x+1 如图,?ABCD的顶点A、B、C、D在⊙O上,顶点C在⊙O的直径BE上,∠AEB=20°,连接AE,则∠ADC的度数为70°.
如图,?ABCD的顶点A、B、C、D在⊙O上,顶点C在⊙O的直径BE上,∠AEB=20°,连接AE,则∠ADC的度数为70°.