Question

18．如图1，已知矩形ABCD的顶点A与点O重合，AD，AB分别在x轴，y轴上，且AD=2，AB=3，抛物线y=-x²+bx+c经过坐标原点O和x轴上另一点E（4，0）．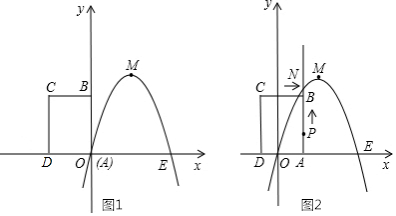

（1）求该抛物线的解析式，并求当x取何值时，该抛物线有最大值，这个最大值是多少？
（2）将矩形ABCD以每秒1个单位长度的速度从图1所示的位置沿x轴的正方向匀速平行移动，同时一动点P也以相同的速度从A点出发向沿射线AB匀速移动，设它们运动的时间为t秒（t＞0），直线AB与该抛物线的交点为N（如图2所示）．
①若抛物线y=-x²+bx+c经过矩形BC边的中点，求t的值；
②在运动过程中，当以P、N、C、D为顶点的四边形是平行四边形时，P点坐标为（t，t）（用含t的式子表示），并求此时t的值．

Answer 1

分析 （1）由O、E的坐标可求得b、c的值，可求得抛物线解析式，再利用二次函数的性质可求得其最大值；
（2）①由题意可设BC的中点为F，则F点坐标为（t-1，3），代入抛物线解析式可求得t的值；②由平行四边形的性质可知PN=CD=3，用t可分别表示出P、N的坐标，再由PN的长度可求得t的值．

解答 解：
（1）∵抛物线y=-x²+bx+c经过坐标原点O和x轴上另一点E（4，0），
∴c=0，b=4，
∴抛物线解析式为y=-x²+4x=-（x-2）²+4，
∴当x=2时，抛物线有最大值，最大值为4；
（2）①设BC的中点为F，则F（t-1，3），
当抛物线过F点时，则有3=-（t-1）²+4（t-1），解得t=2或t=4，
即当t的值为2或4时，抛物线经过矩形BC边的中点；
②∵矩形ABCD，PN∥CD，
∴当点P运动到PN=CD=3时，四边形PNCD为平行四边形，
∵点A在x轴的非负轴上，且N在抛物线上，
∴OA=AP=t，
∴P（t，t），N（t，-t²+4t），
当0≤t≤3时，PN=-t²+4t-t=-t²+3t，由-t²+3t=3可知该方程无实数根，
当t＞3时，PN=t-（-t²+4t）=t²-3t，由t²-3t=3解得t=$\frac{3+\sqrt{21}}{2}$或t=$\frac{3-\sqrt{21}}{2}$＜0（不合题意，舍去），
故答案为：（t，t）．

点评 本题为二次函数的综合应用，主要涉及待定系数法、二次函数的性质、矩形的性质、平行四边形的性质及方程思想等知识．在（1）中注意待定系数法的应用，在（2）①中，用t表示出F点的坐标是解题的关键，在（2）②中由平行四边形的性质得到PN的长是解题的关键．本题考查知识点较多，综合性较强，难度适中．