题目内容
11.观察分析下列方程:①x+$\frac{2}{x}$=3;②x+$\frac{6}{x}$=5;③x+$\frac{12}{x}$=7.请利用它们所蕴含的规律,求关于x的方程x+$\frac{{n}^{2}+n}{x-4}$=2n+5(n为正整数)的根,你的答案是x=n+4或x=n+5.分析 已知方程变形后,归纳总结得到一般性规律,求出所求方程的解即可
解答 解:x+$\frac{1×2}{x}$=3,解得:x=2或x=1;
x+$\frac{2×3}{x}$=5,解得:x=2或x=3;
x+$\frac{3×4}{x}$=7,解得:x=3或x=4,
得到规律x+$\frac{mn}{x}$=m+n的解为:x=m或x=n,
所求方程整理得:x-4+$\frac{n(n+1)}{x-4}$=2n+1,
根据规律得:x-4=n或x-4=n+1,
解得:x=n+4或x=n+5.
故答案为:x=n+4或x=n+5
点评 此题考查了分式方程的解,弄清题中的规律是解本题的关键.

练习册系列答案
相关题目
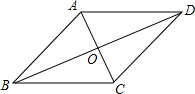 如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$.
如图,平行四边形ABCD中,对角线AC、BD相交于点O,现从以下四个式子①AB=BC,②AC=BD,③AC⊥BD,④∠ABC=90°中,任取一个作为条件,即可推出平行四边形ABCD是菱形的概率为$\frac{1}{2}$.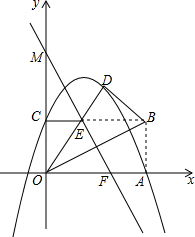 如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),沿着OB翻折△OAB,设翻折后的点A的应对点为点D,OD与BC交于点E,点M在y轴上,直线ME与x轴相交于点F,且∠EMC与∠MOB互余,经过点A,C,D的抛物线的解析式为y=ax2+bx+c.
如图,在平面直角坐标系中,矩形OABC的顶点A,C分别在x轴和y轴的正半轴上,顶点B的坐标为(2m,m),沿着OB翻折△OAB,设翻折后的点A的应对点为点D,OD与BC交于点E,点M在y轴上,直线ME与x轴相交于点F,且∠EMC与∠MOB互余,经过点A,C,D的抛物线的解析式为y=ax2+bx+c.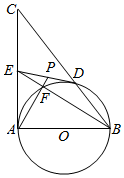 如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
如图,在△ABC中,∠BAC=90°,E是AC的中点,AB是⊙O的直径,⊙O交BC于点D,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.