题目内容
20.阅读材料:善思考的小军在解方程组$\left\{\begin{array}{l}{2x+5y=3①}\\{4x+11y=5②}\end{array}\right.$时,采用了一种“整体代入”的解法:解:将方程②变形:4x+10y+y=5,即2(2x+5y)+y=5 ③
把方程①代入③,得:2×3+y=5,所以y=-1
把y=-1代入①得,x=4,
所以方程组的解为 $\left\{\begin{array}{l}x=4\\ y=-1\end{array}\right.$.
请你模仿小军的“整体代入”法解方程组$\left\{\begin{array}{l}3x-2y=5\\ 9x-4y=19\end{array}\right.$.
分析 方程组中第二个方程变形后,将第一个方程代入求出x的值,进而求出y的值,得到方程组的解.
解答 解:$\left\{\begin{array}{l}{3x-2y=5①}&{\;}\\{9x-4y=19②}&{\;}\end{array}\right.$
将方程②变形:3(3x-2y)+2y=19.
将方程①代入③,得3×5+2y=19.y=2
把y=2代入①得 x=3
∴方程组的解为$\left\{\begin{array}{l}x=3\\ y=2\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
相关题目
11.二元一次方程2x+y=8的正整数解有( )
| A. | 2组 | B. | 3组 | C. | 4组 | D. | 5组 |
12.最薄的金箔的厚度为0.000000091m,用科学记数法表示为( )m.
| A. | 9.1×10-10 | B. | 9.1×10-9 | C. | 9.1×10-8 | D. | 9.1×10-7 |
10.给出下列图形名称:线段、直角、等腰三角形、平行四边形、长方形.这五种图形中是轴对称图形的有
( )
( )
| A. | 1 个 | B. | 2个 | C. | 3个 | D. | 4个 |
 如图L形图案由4个全等的正方形组成,在图案中改变1个正方形的位置,画成新图案,使它既成中心对称图形,又成轴对称图形(要求:被移走的正方形里面标注X,后补上的正方形画实线)
如图L形图案由4个全等的正方形组成,在图案中改变1个正方形的位置,画成新图案,使它既成中心对称图形,又成轴对称图形(要求:被移走的正方形里面标注X,后补上的正方形画实线)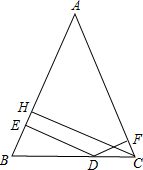 已知:在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,
已知:在△ABC中,AB=AC,点D、E、F分别在边BC、AB、AC上,