题目内容
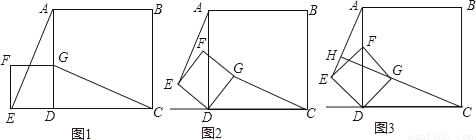
(1)如图1,正方形ABCD和正方形DEFG,G在AD边上,E在CD的延长线上.求证:AE=CG,AE⊥CG;
(2)如图2,若将图1中的正方形DEFG绕点D顺时针旋转角度θ(0°<θ<90°),此时AE=CG还成立吗?若成立,请给予证明;若不成立,请说明理由;
(3)如图3,当正方形DEFG绕点D顺时针旋转45°时,延长CG交AE于点H,当AD=4,DG=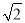 时,求线段CH的长.
时,求线段CH的长.
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
抛物线y=ax2+bx+c上部分点的横坐标x,纵坐标y,的对应值如下表:
x | … | -2 | -1 | 0 | 1 | 2 | … |
y | … | 0 | -4 | -4 | 0 | 8 | … |
(1)根据上表填空:
①抛物线与x轴的交点坐标是_________和_________;
②抛物线经过点(-3,_________);
(2)试确定抛物线y=ax2+bx+c的解析式.
(1)①(-2,0),(1,0);②8;(2)所求抛物线解析式为y=2x2+2x-4. 【解析】试题分析: (1)①根据表格中函数值y=0即可得到与x轴的交点坐标; ②观察表格可知抛物线的对称轴为x=,由此可知(2,8)与(-3,8)关于对称轴对称,从而可得; (2)依题意设抛物线解析式为y=a(x+2)(x-1),代入点(0,-4)即可求得. 试题解析:(1)①观察表格可...2017年春节即将来临,甲、乙两单位准备组织退休职工到李坑景区游玩.甲、乙两单位共102人,其中甲单位人数多于乙单位人数,且甲单位人数不够100人.经了解,李坑景区的门票价格如下表:
数量(张) | 1﹣50 | 51﹣100 | 101张及以上 |
单价(元/张) | 60元 | 50元 | 40元 |
如果两单位分别单独购买门票,一共应付5500元.
(1)如果甲、乙两单位联合起来购买门票,那么比各自购买门票共可以节省多少钱?
(2)甲、乙两单位各有多少名退休职工准备参加游玩?
(3)如果甲单位有12名退休职工因身体原因不能外出游玩,那么你有几种购买方案,通过比较,你该如何购买门票才能最省钱?
(1)甲、乙两单位联合起来购买门票比各自购买门票共可以节省1420元; (2)甲单位有62人,乙单位有40人;(3)甲乙两单位联合起来选择按40元一次购买101张门票最省钱. 【解析】试题分析:(1)运用分别购票的费用和﹣联合购票的费用就可以得出结论; (2)设甲单位有退休职工x人,则乙单位有退休职工(102﹣x)人,根据“如果两单位分别单独购买门票,一共应付5500元”建立方程求出其...

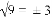 B. (m2)3=m5 C. a2•a3=a5 D. (x+y)2=x2+y2
B. (m2)3=m5 C. a2•a3=a5 D. (x+y)2=x2+y2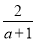 ﹣
﹣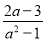 )÷
)÷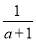 的值,其中a=2sin60°+tan45°.
的值,其中a=2sin60°+tan45°. x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )
x+8与x轴、y轴分别交于A.B两点,点M是OB上一点,若直线AB沿AM折叠,点B恰好落在x轴上的点C处,则点M的坐标是( )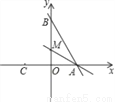
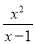 ﹣
﹣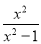 )÷
)÷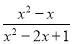 ,其中x是方程3x2﹣x﹣1=0的根.
,其中x是方程3x2﹣x﹣1=0的根.