题目内容
一名学生取x等于某自然数代入下面的某个二次三项式，计算后得到一个完全平方数，则代入的二次三项式是（ ）
| A、x2+11x+2 |
| B、x2+5x+7 |
| C、x2+7x+10 |
| D、x2+9x+18 |
考点：完全平方数
专题：
分析：利用完全平方数的性质得出只有x2+11x+2可能取值平方数，进而得出答案．
解答：解：∵（x+2）2＜x2+5x+7＜（x+3）2，
（x+3）2＜x2+7x+10＜（x+4）2，
（x+4）2＜x2+9x+18＜（x+5）2，
∴当x取自然数时，x2+5x+7，x2+7x+10，x2+9x+18，
都介于两个相邻的平方数之间，故不可能是平方数，
因此，只有x2+11x+2可能取值平方数，
当x=23时，x2+11x+2=784=282，
故选：A．
（x+3）2＜x2+7x+10＜（x+4）2，
（x+4）2＜x2+9x+18＜（x+5）2，
∴当x取自然数时，x2+5x+7，x2+7x+10，x2+9x+18，
都介于两个相邻的平方数之间，故不可能是平方数，
因此，只有x2+11x+2可能取值平方数，
当x=23时，x2+11x+2=784=282，
故选：A．
点评：此题主要考查了完全平方数的特征，得出各式的取值范围是解题关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
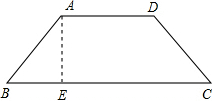如图，铁路路基的横截面是等腰梯形，斜坡AB的坡度为1：
如图所示，已知∠ACB=∠CBD=90°，AC=4cm，BC=3cm，那么边BD的长度为多少时，△ACB与△CBD相似？