题目内容
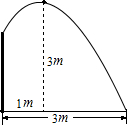 要修建一个圆形水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离地中心3m.
要修建一个圆形水池,在池中心竖直安装一根水管,在水管的顶端安装一个喷水头,使喷出的抛物线形水柱在与池中心的水平距离为1m处达到最高,高度为3m,水柱落地处离地中心3m.(1)求抛物线解析式;
(2)水管应多长.
考点:二次函数的应用
专题:
分析:(1)以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系,设抛物线的解析式为y=a(x-1)2+3,将(3,0)代入求得a值;
(2)由题意可得,x=0时得到的y值即为水管的长.
(2)由题意可得,x=0时得到的y值即为水管的长.
解答:解:(1)以池中心为原点,竖直安装的水管为y轴,与水管垂直的为x轴建立直角坐标系.
由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:y=a(x-1)2+3,
代入(3,0)求得:a=-
(x-1)2+3.
将a值代入得到抛物线的解析式为:y=-
(x-1)2+3;
(2)令x=0,则y=
=2.25.
故水管长为2.25m.
由于在距池中心的水平距离为1m时达到最高,高度为3m,
则设抛物线的解析式为:y=a(x-1)2+3,
代入(3,0)求得:a=-
| 3 |
| 4 |
将a值代入得到抛物线的解析式为:y=-
| 3 |
| 4 |
(2)令x=0,则y=
| 9 |
| 4 |
故水管长为2.25m.
点评:本题考查了二次函数在实际生活中的运用,重点是二次函数解析式的求法,利用顶点式求出解析式是解题关键.

练习册系列答案
相关题目
 如图,在△ABC中,BD⊥AC,EF⊥AC,垂足分别为点D,F.若∠DEF=∠CBD,DE∥CB吗?为什么?
如图,在△ABC中,BD⊥AC,EF⊥AC,垂足分别为点D,F.若∠DEF=∠CBD,DE∥CB吗?为什么? ⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证:
⊙O1与⊙O2外切于点P,过P点的直线AB与⊙O1和⊙O2相交于A、B,⊙O1的切线AD与⊙O2相交于点C、D.求证: