题目内容
2.数学课上,王老师出示问题:如图1,将边长为5的正方形纸片ABCD折叠,使顶点A落在边CD上的点P处(点P与C、D不重合),折痕为EF,折叠后AB边落在PQ的位置,PQ与BC交于点G.(1)观察操作结果,在图1中找到一个与△DEP相似的三角形,并证明你的结论;
(2)当点P在边CD的什么位置时,△DEP与△CPG面积的比是9:25?请写出求解过程;
(3)将正方形换成正三角形,如图2,将边长为5的正三角形纸片ABC折叠,使顶点A落在边BC上的点P处(点P与B、C不重合),折痕为EF,当点P在边BC的什么位置时,△BEP与△CPF面积的比是9:25?请写出求解过程.

分析 (1)根据∠DEP=∠GPC,∠D=∠C=90°,判定△DEP∽△CPG即可;
(2)根据相似三角形的面积之比等于相似比的平方,可得DP:GC=3:5,再设PD=3x,得出CG=5x,PC=5-3x,DE=$\frac{3}{5}$PC=3-$\frac{9}{5}$x,EP=2+$\frac{9}{5}$x,最后在Rt△DEP中,根据勾股定理,列出关于x的方程进行求解即可;
(3)根据两角对应相等,判定△BEP∽△CPF,再设EP=3x,FP=5x,得出FC=5-5x,EB=5-3x,BP=$\frac{3}{5}$CF=3-3x,PC=2+3x,最后根据相似三角形对应边成比例,列出方程求解即可.
解答  解:(1)△DEP∽△CPG.
解:(1)△DEP∽△CPG.
∵∠EPG=90°,
∴∠EPD+∠GPC=90°,∠EPD+∠DEP=90°,
∴∠DEP=∠GPC,
∵∠D=∠C=90°,
∴△DEP∽△CPG;
(2)∵△DEP∽△CPG,
∴S△DEP:S△CPG=9:25,
∴DP:GC=3:5,
设PD=3x,则CG=5x,PC=5-3x,DE=$\frac{3}{5}$PC=3-$\frac{9}{5}$x,
∴EP=2+$\frac{9}{5}$x,
∴Rt△DEP中,(3-$\frac{9}{5}$x)2+(3x)2=(2+$\frac{9}{5}$x)2,
解得x1=$\frac{5}{3}$(舍去),x2=$\frac{1}{3}$,
∴DP=3x=1,
即当DP=1时,△DEP与△CPG面积的比是9:25;
(3)由题可得,∠B=∠C=∠EPF=60°,
∴∠BEP+∠BPE=∠CPF+∠BPE=120°,
∴∠BEP=∠CPF,
∴△BEP∽△CPF,
设EP=3x,FP=5x,则FC=5-5x,EB=5-3x,BP=$\frac{3}{5}$CF=3-3x,
∴PC=2+3x,
∴$\frac{EB}{PC}$=$\frac{5-3x}{2+3x}$=$\frac{3}{5}$,
解得x=$\frac{19}{24}$,
∴PC=2+3x=$\frac{35}{8}$.
即当PC=$\frac{35}{8}$时,△BEP与△CPF面积的比是9:25.
点评 本题主要考查了相似三角形的综合应用,解题时注意:有两组角对应相等的两个三角形相似;相似三角形的面积的比等于相似比的平方.解决问题的关键是运用方程思想进行求解.

 名校课堂系列答案
名校课堂系列答案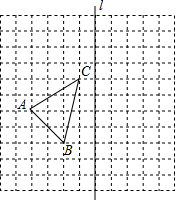 如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
如图,在11×11的正方形网格中,每个小正方形的边长都为1,网格中有一个格点△ABC(即三角形的顶点都在格点上).
 如图,已知点P是△ABC的重心,过P作AB的平行线DE,分别交AC于点D、交BC于点E;作DF∥BC,交AB于点F,若△ABC的面积为18,则?BEDF的面积为8.
如图,已知点P是△ABC的重心,过P作AB的平行线DE,分别交AC于点D、交BC于点E;作DF∥BC,交AB于点F,若△ABC的面积为18,则?BEDF的面积为8. 如图,秋千链子AB的长度为3m,静止时的秋千踏板(厚度忽略不计)距地面DE为0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为53°,求秋千踏板与地面的最大距离.(sin53°≈0.80,cos53°≈0.60)
如图,秋千链子AB的长度为3m,静止时的秋千踏板(厚度忽略不计)距地面DE为0.5m,秋千向两边摆动时,若最大摆角(摆角指秋千链子与铅垂线的夹角)约为53°,求秋千踏板与地面的最大距离.(sin53°≈0.80,cos53°≈0.60) 如图,抛物线y=-(x-1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E.
如图,抛物线y=-(x-1)2+4与x轴交于点A,B(点A在点B的左侧),与y轴交于点C,CD∥x轴交抛物线另一点D,连结AC,DE∥AC交边CB于点E. 已知抛物线y=-x2+bx-c的部分图象如图所示.
已知抛物线y=-x2+bx-c的部分图象如图所示.