Question

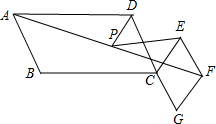如图，?ABCD∽?CEFG，

AD

EF

=

AB

CE

，且

AC

BD

=k，P为AF的中点，探究线段DP、EP的数量关系．

Answer 1

分析：此题需要从相似多边形和相似三角形的角度入手求解；首先连接AC、BD，EG、CF，设AC、BD的交点为M，EG、CF的交点为N，连接MP、NP；根据平行四边形的对角线互相平分得：MP、NP是△ACF的两条中位线，那么四边形MPNC是平行四边形，然后通过证△DPM∽△PEN来求得DP、EP的数量关系．

解答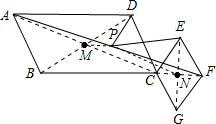：解：如图，连接AC、BD交于点M，连接EG、CF交于点N；
连接MP、PN，则MP、PN是△ACF的中位线；
故PN∥MC、MP∥CN，且PN=

1

2

AC、MP=

1

2

CF；
∴四边形MPCN是平行四边形，
∴∠PMC=∠CNP，
由于?ABCD∽?CEFG，得∠AMD=∠ENF，则∠DMP=∠ENP；
又∵

DM

PN

=

1 2 BD

1 2 AC

=

1

k

，

MP

EN

=

1 2 CF

1 2 EG

=

1

k

，
∴

DM

PN

=

MP

EN

=

1

k

，
∴△DMP∽△PNE，
得：

DP

PE

=

1

k

，即PE=kPD；
故DP、PE的数量关系为：PE=kPD．

点评：此题主要考查的是相似三角形和相似多边形的应用，还涉及到平行四边形的判定和性质、三角形中位线定理等知识，难度较大．