题目内容
如图①,ABCD是一张正方形纸片,E、F分别为AB、CD的中点,沿过点D的折痕将A角翻折,使得点A落在EF上的A’处(如图②),折痕交AE于点G,那么∠ADG等于多少度?(写出计算步骤)
分析:根据正方形的性质,即可得∠C=∠A=90°,AD=BC=CD=AB,又由E、F分别为AB、CD的中点,即可得在Rt△A′DF中,由sin∠FA′D=
=
,即可求得∠DA′F的度数,然后根据折叠的性质与平行线的性质,即可求得∠ADG的度数.
| DF |
| A′D |
| 1 |
| 2 |
解答:解:∵四边形ABCD是正方形,
∴∠C=∠A=90°,AD=BC=CD=AB,
∵E、F分别为AB、CD的中点,
∴EF∥BC,
∴四边形ADFE是矩形,
∴∠EFD=90°,FD=
CD=
AD,
根据折叠的性质:A′D=AD,
∴在Rt△FAD中,sin∠FA′D=
=
,
∴∠FA′D=30°,
∴∠A′DA=∠FA′D=30°,
∴∠ADG=∠A′DG=
∠ADA′=
×30°=15°.
∴∠C=∠A=90°,AD=BC=CD=AB,
∵E、F分别为AB、CD的中点,
∴EF∥BC,
∴四边形ADFE是矩形,
∴∠EFD=90°,FD=
| 1 |
| 2 |
| 1 |
| 2 |

根据折叠的性质:A′D=AD,
∴在Rt△FAD中,sin∠FA′D=
| DF |
| A′D |
| 1 |
| 2 |
∴∠FA′D=30°,
∴∠A′DA=∠FA′D=30°,
∴∠ADG=∠A′DG=
| 1 |
| 2 |
| 1 |
| 2 |
点评:此题考查了正方形的性质,折叠的性质,平行线的性质以及三角函数的性质等知识.此题难度适中,解题的关键是数形结合思想的应用.

练习册系列答案
相关题目
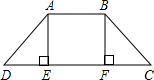 如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问AD与BC是否相等?说明你的理由.
如图,四边形ABCD是一防洪堤坝的横截面,AE⊥CD,BF⊥CD,且AE=BF,∠D=∠C,问AD与BC是否相等?说明你的理由.

 如图,四边形ABCD是一张矩形纸片,AB=6,AD=8,在AB上取一点E,将纸片沿DE翻折,使点A落在BD上的点F处,求AE的长.
如图,四边形ABCD是一张矩形纸片,AB=6,AD=8,在AB上取一点E,将纸片沿DE翻折,使点A落在BD上的点F处,求AE的长.