题目内容
16.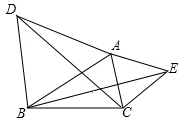 如图,分别从△ABC的边AB,AC为一边向外作等边三角形ABD,ACE,连接BE,DC,BE与DC相等吗?请说明理由.
如图,分别从△ABC的边AB,AC为一边向外作等边三角形ABD,ACE,连接BE,DC,BE与DC相等吗?请说明理由.
分析 由△ABD与△ACE都为等边三角形,利用等边三角形的性质得到两对边相等,∠BAD=∠CAE=60°,利用等式的性质得到∠DAC=∠BAE,利用SAS可得出△ABE≌△ADC,然后根据全等三角形的性质即可得到结论.
解答 解:BE=CD,
理由:∵△ACE和△ABD都为等边三角形,
∴AB=AD,AE=AC,∠DAB=60°,∠EAC=60°,
∴∠DAB+∠BAC=∠EAC+∠BAC,
即∠BAE=∠DAC.
在△DAC和△BAE中,
$\left\{\begin{array}{l}{AB=AD}\\{∠BAE=∠DAC}\\{AE=AC}\end{array}\right.$,
∴△ABE≌△ADC(SAS),
∴BE=CD.
点评 此题考查了等边三角形的性质,全等三角形的判定与性质,以及三角形的外角性质,熟练掌握等边三角形的判定与性质是解本题的关键.

练习册系列答案
 鹰派教辅衔接教材河北教育出版社系列答案
鹰派教辅衔接教材河北教育出版社系列答案 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
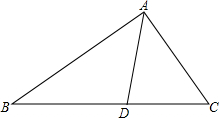 如图所示,已知在△ABC中,AB>AC,AD平分∠BAC,交BC于点D.求证:BD>DC.
如图所示,已知在△ABC中,AB>AC,AD平分∠BAC,交BC于点D.求证:BD>DC.