题目内容
1.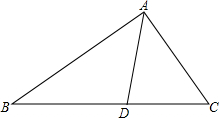 如图所示,已知在△ABC中,AB>AC,AD平分∠BAC,交BC于点D.求证:BD>DC.
如图所示,已知在△ABC中,AB>AC,AD平分∠BAC,交BC于点D.求证:BD>DC.
分析 过B做BP∥AC,交AD延长线于P,根据平行线的性质得到∠DAC=∠BPD,由角平分线定义得到∠DAC=∠BAD,等量代换得到∠DAC=∠BAD=∠BPD,根据等腰三角形的性质得到BP=AB,推出△BDP∽△ADC,根据相似三角形的性质得到$\frac{BP}{AC}=\frac{BD}{CD}$,等量代换得到$\frac{AB}{AC}=\frac{BD}{CD}$,根据等式的性质即可得到结论.
解答 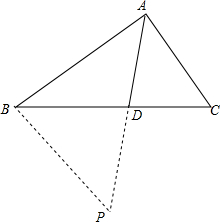 证明:过B做BP∥AC,交AD延长线于P,
证明:过B做BP∥AC,交AD延长线于P,
∴∠DAC=∠BPD,
∵AD平分∠BAC,
∴∠DAC=∠BAD,
∴∠DAC=∠BAD=∠BPD,
∴BP=AB,
∵∠BDP=∠ADC,
∴△BDP∽△ADC,
∴$\frac{BP}{AC}=\frac{BD}{CD}$,
∵BP=AB,
∴$\frac{AB}{AC}=\frac{BD}{CD}$,
∵AB>AC,
∴$\frac{AB}{AC}=\frac{BD}{CD}$>1,
∴BD>DC.
点评 本题考查了相似三角形的判定和性质,角平分线的定义,平行线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 习题精选系列答案
习题精选系列答案
相关题目
 如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为π-$\frac{4\sqrt{3}}{3}$.
如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为π-$\frac{4\sqrt{3}}{3}$.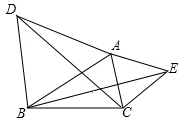 如图,分别从△ABC的边AB,AC为一边向外作等边三角形ABD,ACE,连接BE,DC,BE与DC相等吗?请说明理由.
如图,分别从△ABC的边AB,AC为一边向外作等边三角形ABD,ACE,连接BE,DC,BE与DC相等吗?请说明理由.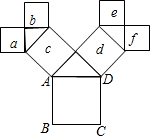 如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形a,b,c,d,e,f的面积和为32,则最大的正方形ABCD的边长为4.
如图,所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形a,b,c,d,e,f的面积和为32,则最大的正方形ABCD的边长为4.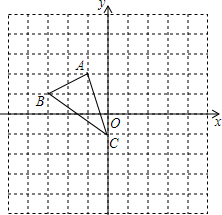 如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).
如图,在平面直角坐标系网格中,△ABC的顶点都在格点上,点C坐标(0,-1).