题目内容
13.如图,在平面直角坐标系中,已知△AOB是等边三角形,点A的坐标是(0,4),点B在第一象限,点P是x轴上的一个动点,连结AP,并把△AOP绕着点A按逆时针方向旋转,使边AO与AB重合,得到△ABD.(1)求直线AB的解析式;
(2)当点P运动到点$(\sqrt{3},0)$时,求此时DP的长及点D的坐标.
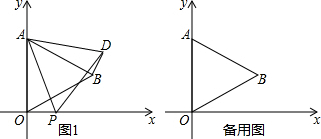
分析 (1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F,根据题意得到BF=OE=2,利用等边三角形的性质进而求出OF的长,确定出B的坐标,设直线AB解析式为y=kx+b,把A与B坐标代入求出k与b的值,即可确定出直线AB解析式;
(2)由△ABD由△AOP旋转得到,利用旋转的性质得到两三角形全等,利用全等三角形对应边相等,对应角相等得到AP=AD,∠DAB=∠PAO,进而得到三角形ADP为等腰直角三角形,求出AP的长,即为等边三角形的边长,如图1,过点D作DH⊥x轴于点H,延长EB交DH于点G,可得BG⊥DH,在直角三角形BDG中,求出BG与DG的长,进而确定出OH与DH的长,确定出D坐标即可.
解答  解:(1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F,
解:(1)如图1,过点B作BE⊥y轴于点E,作BF⊥x轴于点F,
由已知得:BF=OE=2,OF=$\sqrt{{4}^{2}-{2}^{2}}$=2$\sqrt{3}$,
∴点B的坐标是(2$\sqrt{3}$,2),
设直线AB的解析式是y=kx+b,则有$\left\{\begin{array}{l}{b=4}\\{2\sqrt{3}k+b=2}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{k=-\frac{\sqrt{3}}{3}}\\{b=4}\end{array}\right.$,
∴直线AB的解析式是y=-$\frac{\sqrt{3}}{3}$x+4;
(2)∵△ABD由△AOP旋转得到,
∴△ABD≌△AOP,
∴AP=AD,∠DAB=∠PAO,
∴∠DAP=∠BAO=60°,
∴△ADP是等边三角形,
∴DP=AP=$\sqrt{{4}^{2}+(\sqrt{3})^{2}}$=$\sqrt{19}$,
如图1,过点D作DH⊥x轴于点H,延长EB交DH于点G,可得BG⊥DH,
在Rt△BDG中,∠BGD=90°,∠DBG=60°,BD=OP=$\sqrt{(\sqrt{19})^{2}{-4}^{2}}$=$\sqrt{3}$,
∴BG=BD•cos60°=$\sqrt{3}$×$\frac{1}{2}$=$\frac{\sqrt{3}}{2}$,DG=BD•sin60°=$\sqrt{3}$×$\frac{\sqrt{3}}{2}$=$\frac{3}{2}$,
∴OH=EG=$\frac{5\sqrt{3}}{2}$,DH=$\frac{7}{2}$,
∴点D的坐标为($\frac{5\sqrt{3}}{2}$,$\frac{7}{2}$).
点评 此题属于一次函数综合题,涉及的知识有:待定系数法确定一次函数解析式,坐标与图形性质,等边三角形的判定与性质,旋转的性质,锐角三角函数定义,以及勾股定理,熟练掌握性质及定理是解本题的关键.

| A. | 120° | B. | 30° | C. | 45° | D. | 60° |
| A. | sin60°=$\frac{\sqrt{3}}{2}$ | B. | tan30°•tan60°=1 | ||
| C. | sin230°+cos230°=1 | D. | sin$\frac{1}{2}$=30° |
| A. | 4 | B. | -4 | C. | ±4 | D. | 以上结果都不对 |
| A. | M>N | B. | M=N | C. | M<N | D. | 无法确定 |
| A. | 1.37×103米 | B. | 13.7×103米 | C. | 1.37×104米 | D. | 13.7×102米 |
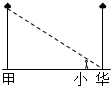 如图,甲、乙两盏路灯底部间的距离是25米,一天晚上,当小华走到距路灯乙底部4米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.6米,那么路灯甲的高为10米.
如图,甲、乙两盏路灯底部间的距离是25米,一天晚上,当小华走到距路灯乙底部4米处时,发现自己的身影顶部正好接触路灯乙的底部.已知小华的身高为1.6米,那么路灯甲的高为10米.