题目内容
 如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.
如图,PA,PB分别与⊙O相切于点A,B,∠APB=60°,连接AO,BO.(1)
 |
| AB |
(2)若OA=3,求阴影部分的面积.
考点:切线的性质,扇形面积的计算
专题:
分析:(1)根据切线的性质可以证得∠OAP=∠OBP=90°,根据四边形内角和定理求解;
(2)首先证明直角△OAP≌直角△OBP,然后求得△OPA的面积,即求得四边形OAPB的面积,再求得扇形OAB的面积,即可求得阴影部分的面积.
(2)首先证明直角△OAP≌直角△OBP,然后求得△OPA的面积,即求得四边形OAPB的面积,再求得扇形OAB的面积,即可求得阴影部分的面积.
解答:(1)解:∵PA,PB分别与⊙O相切于点A,B,
∴∠OAP=∠OBP=90°,
∵∠APB=60°,
∴∠AOB=360°-90°-90°-60°=120°;
故答案为120°;
(2)证明:连接OP.
在Rt△OAP和Rt△OBP中,
,
∴Rt△OAP≌Rt△OBP(HL),
∴∠OPA=∠OPB=
∠APB=30°,
在Rt△OAP中,OA=3,
∴AP=3
,
∴S△OPA=
×3×3
=
,
∴S阴影=2×
-
=9
-3π.
∴∠OAP=∠OBP=90°,
∵∠APB=60°,
∴∠AOB=360°-90°-90°-60°=120°;
故答案为120°;
(2)证明:连接OP.
在Rt△OAP和Rt△OBP中,
|
∴Rt△OAP≌Rt△OBP(HL),
∴∠OPA=∠OPB=
| 1 |
| 2 |
在Rt△OAP中,OA=3,
∴AP=3
| 3 |
∴S△OPA=
| 1 |
| 2 |
| 3 |
9
| ||
| 2 |
∴S阴影=2×
9
| ||
| 2 |
| 120π×32 |
| 360 |
| 3 |
点评:本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.

练习册系列答案
相关题目
 用反正法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )
用反正法证明命题“如图,如果AB∥CD,AB∥EF,那么CD∥EF”时,证明的第一个步骤是( )| A、假设AB不平行于CD |
| B、假设AB不平行于EF |
| C、假设CD∥EF |
| D、假设CD不平行于EF |
下列等式从左到右变形,属于因式分解的是( )
| A、a(x-y)=ax-ay | ||
| B、x2+2x-1=x(x+2)-1 | ||
| C、a2-a=a(a-1) | ||
D、a2-1=a(a-
|
满足下列条件的△ABC不是直角三角形的是( )
A、BC=1,AC=2,AB=
| ||
| B、BC:AC:AB=3:4:5 | ||
| C、∠A+∠B=∠C | ||
| D、∠A:∠B:∠C=3:4:5 |
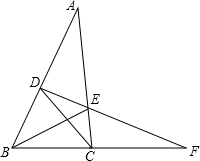 如图,在△ABC,点D、E分别在AB、AC上,连结DE并延长交BC的延长线于点F,连结DC、BE,若∠BDE+∠BCE=180°.请写出图中的两对相似三角形(不另外添加字母和线),并选择其中的一对进行证明.
如图,在△ABC,点D、E分别在AB、AC上,连结DE并延长交BC的延长线于点F,连结DC、BE,若∠BDE+∠BCE=180°.请写出图中的两对相似三角形(不另外添加字母和线),并选择其中的一对进行证明. 如图,一个转盘被分成红黄两种颜色的两个扇形(阴影部分为红),红色扇形的圆心角为150°,在圆心处固定一根指针.转动转盘后任其自由停止,则指针指向红色扇形的概率是
如图,一个转盘被分成红黄两种颜色的两个扇形(阴影部分为红),红色扇形的圆心角为150°,在圆心处固定一根指针.转动转盘后任其自由停止,则指针指向红色扇形的概率是 若关于x的不等式x-m≥-1的解集如图所示,试求-3x+m>6的解.
若关于x的不等式x-m≥-1的解集如图所示,试求-3x+m>6的解.