题目内容
3．在△ABC中，AB=AC，OB=OC，且点A到BC的距离为8，点O到BC的距离为4，则AO的长为4或12．分析 先利用AB=AC，OB=OC可判断点A、O都在BC的垂直平分线上，然后分类讨论：当点O在△ABC的内部时，易得AO=2cm；当点O在△ABC的外部时，易得AO=10cm．
解答 解：∵OB=OC，
∴点O在BC的垂直平分线上，
而AB=AC，
∴点A在BC的垂直平分线上，
当点O在△ABC的内部时，AO=8-4=4；
当点O在△ABC的外部时，AO=8+4=12．
故答案为：4或12．
点评 本题考查了等腰三角形的性质：等腰三角形的两腰相等，等腰三角形的两个底角相等，等腰三角形的顶角平分线、底边上的中线、底边上的高相互重合．
练习册系列答案
相关题目
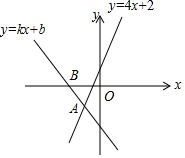如图，直线y=kx+b与直线y=4x+2相交于点A（-1，-2），则不等式（k-4）x＜2-b的解集为x＞-1．
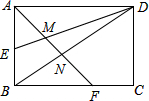如图，矩形ABCD的边长AD=3，AB=2，E为AB的中点，F在边BC上，且BF=2FC，AF分别与DE、DB相交于点M，N，则MN的长为$\frac{9}{20}\sqrt{2}$．
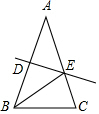如图，在△ABC中，AB=AC=10cm，DE是AB的垂直平分线，分别交AB、AC于D、E两点．若BC=6cm，则△BCE的周长是16 cm．