题目内容
 如图矩形ABCD中,AB=1,AD=
如图矩形ABCD中,AB=1,AD=| 2 |
分析:连接AE.根据题意知AE=AD=
,再利用勾股定理可计算出BE=1,∠BAE=45°,则∠DAE=45°,然后利用扇形面积公式计算出扇形面积,再利用三角形面积公式计算出三角形面积,阴影部分的面积等于矩形的面积减去Rt△ABE的面积和扇形ADE的面积.
| 2 |
解答: 解:连接AE.
解:连接AE.
根据题意,知AE=AD=
.
∵AB=1,AE=
,
∴BE=
=1.
∴AB=BE,
∴∠BAE=(180°-90°)÷2=45°.
则∠DAE=90°-45°=45°,
S△ABE=
×1×1=
,
S扇形ADE=
=
,
则阴影部分的面积=
-
-
.
 解:连接AE.
解:连接AE.根据题意,知AE=AD=
| 2 |
∵AB=1,AE=
| 2 |
∴BE=
(
|
∴AB=BE,
∴∠BAE=(180°-90°)÷2=45°.
则∠DAE=90°-45°=45°,
S△ABE=
| 1 |
| 2 |
| 1 |
| 2 |
S扇形ADE=
45×π×(
| ||
| 360 |
| π |
| 4 |
则阴影部分的面积=
| 2 |
| 1 |
| 2 |
| π |
| 4 |
点评:此题综合运用了等腰直角三角形的面积、扇形的面积公式,关键是熟练掌握扇形面积的计算公式.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中:
14、如图矩形ABCD中BC=8,AB=4,将矩形纸片沿对角线对折,使C点落在F处,BC与AD边交于点E,则下列四个结论中: 如图矩形ABCD中,E为BC上一点,DF⊥AE于F.
如图矩形ABCD中,E为BC上一点,DF⊥AE于F. 29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由.
29、如图矩形ABCD中,DP平分∠ADC交BC于P点,将一个直角三角板的直角顶点放在P点处,且使它的一条直角边过A点,另一条直角边交CD于E.找出图中与PA相等的线段.并说明理由. 如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.
如图矩形ABCD中,过A,B两点的⊙O切CD于E,交BC于F,AH⊥BE于H,连接EF.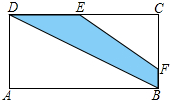 如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=
如图矩形ABCD中,AB=8cm,CB=4cm,E是DC的中点,BF=