题目内容
17.(1)化简:($\frac{1}{x-y}$+$\frac{1}{x+y}$)÷$\frac{{x}^{2}y}{{x}^{2}-{y}^{2}}$(2)先化简,再求值:$\frac{a-2}{a+3}$÷$\frac{{a}^{2}-4}{2a+6}$-$\frac{5}{a+2}$,并选一个你喜欢的数代入求值.
分析 (1)先对括号内的式子通分,然后去括号后,将除法转化为乘法即可解答本题;
(2)根据分式的除法和减法即可化简本题,然后选取合适的a的值代入即可化简本题,注意a不能取2,-2,-3.
解答 解:(1)($\frac{1}{x-y}$+$\frac{1}{x+y}$)÷$\frac{{x}^{2}y}{{x}^{2}-{y}^{2}}$
=$\frac{x+y+x-y}{(x-y)(x+y)}×\frac{(x-y)(x+y)}{{x}^{2}y}$
=$\frac{2x}{{x}^{2}y}$
=$\frac{2}{xy}$;
(2)$\frac{a-2}{a+3}$÷$\frac{{a}^{2}-4}{2a+6}$-$\frac{5}{a+2}$
=$\frac{a-2}{a+3}•\frac{2(a+3)}{(a-2)(a+2)}-\frac{5}{a+2}$
=$\frac{2}{a+2}-\frac{5}{a+2}$
=$\frac{-3}{a+2}$,
当a=1时,原式=$\frac{-3}{1+2}$=-1.
点评 本题考查分式的化简求值,解答此类问题的关键是明确分式化简求值的方法,注意(2)中选取的a的值必须使得原来的分式有意义.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
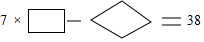
6. 如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
 如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )
如图,在△ABC中,已知∠ADE=∠B,则下列等式成立的是( )| A. | $\frac{AE}{BC}$=$\frac{AD}{BD}$ | B. | $\frac{AD}{AB}$=$\frac{AE}{AC}$ | C. | $\frac{DE}{BC}$=$\frac{AE}{AB}$ | D. | $\frac{DE}{BC}$=$\frac{AD}{AC}$ |
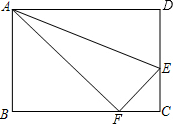 如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3.
如图,折叠长方形纸片ABCD的一边AD,使点D落在BC边上的点F处,AE为折痕.已知AB=8,BC=10,则EC的长为3. 如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D位.测得∠DBO=58°,此时B处距离码头O有多远?
如图,轮船甲位于码头O的正西方向A处,轮船乙位于码头O的正北方向,测得∠CAO=45°.轮船甲自西向东匀速行驶,同时轮船乙沿正北方向匀速行驶,它们的速度分别为45km/h和36km/h,经过0.2h,轮船甲行驶至B处,轮船乙行驶至D位.测得∠DBO=58°,此时B处距离码头O有多远?