题目内容
7. 如图,抛物线与x轴的两个交点分别为A(1,0),B(4,0)与y轴交于点C(0,4),点P为抛物线上的一个动点.
如图,抛物线与x轴的两个交点分别为A(1,0),B(4,0)与y轴交于点C(0,4),点P为抛物线上的一个动点.(1)抛物线的解析式,在平面直角坐标系中画出它的图象;
(2)若∠APB=90°,求P点的坐标.
分析 (1)根据待定系数法,可得函数解析式,根据描点法,可得答案.
(2)根据勾股定理,可得AP2,PB2,再根据勾股定理的逆定理,可得关于a的方程,根据解方程,可得答案.
解答 解:(1)设抛物线的解析式为y=ax2+bx+c,将A,B,C代入函数解析式,得
$\left\{\begin{array}{l}{a+b+c=0}\\{16a+4b+c=0}\\{c=4}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=1}\\{b=-5}\\{c=4}\end{array}\right.$,
抛物线的解析式为y=x2-5x+4,
如图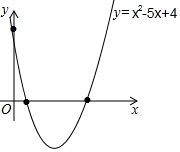 ,
,
(2)设P(m,m2-5m+4),
AP2=(m-1)2+(m2-5m+4)2,BP2=(m-4)2+(m2-5m+4),
由勾股定理逆定理,得AP2+PB2=AB2,
即(m-1)2+(m2-5m+4)2+(m-4)2+(m2-5m+4)=(4-1)2,
化简,得
(m2-5m+4)+(m2-5m+4)2=0,
(m2-5m+4)(m2-5m+5)=0,
因式分解,得
(m-1)(m-4)(m-$\frac{5+\sqrt{5}}{2}$)(m-$\frac{5-\sqrt{5}}{2}$)=0,
于是m1=1(舍),m2=4(舍),m3=$\frac{5+\sqrt{5}}{2}$,m4=$\frac{5-\sqrt{5}}{2}$,
P($\frac{5+\sqrt{5}}{2}$,-1)P($\frac{5-\sqrt{5}}{2}$,-1).
点评 本题考查了二次函数综合题,解(1)的关键是待定系数法,解(2)的关键是勾股定理及勾股定理的逆定理.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
17.我们规定一个物体向右运动为正,向左运动为负.如果该物体向左连续运动两次,每次运动3 米,那么下列算式中,可以表示这两次运动结果的是( )
| A. | (-3)2 | B. | (-3)-(-3) | C. | 2×3 | D. | 2×(-3) |
 如图,已知正方形ABCD的边长为2,以DC为底向正方形外作等腰△DEC,连接AE,以AE为腰作等腰△AEF,使得EA=EF,且∠DEC=∠AEF.
如图,已知正方形ABCD的边长为2,以DC为底向正方形外作等腰△DEC,连接AE,以AE为腰作等腰△AEF,使得EA=EF,且∠DEC=∠AEF. 在我校刚刚结束的缤纷体育节上,初三年级参加了60m迎面接力比赛.假设每名同学在跑步过程中是匀速的,且交接棒的时间忽略不计,如图是A、B两班的路程差y(米)与比赛开始至A班先结束第二棒的时间x(秒)之间的函数图象.则B班第二棒的速度为9米/秒.
在我校刚刚结束的缤纷体育节上,初三年级参加了60m迎面接力比赛.假设每名同学在跑步过程中是匀速的,且交接棒的时间忽略不计,如图是A、B两班的路程差y(米)与比赛开始至A班先结束第二棒的时间x(秒)之间的函数图象.则B班第二棒的速度为9米/秒.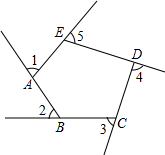 如图∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,∠1=∠2=∠3=∠4=70°,则∠AED=100°.
如图∠1,∠2,∠3,∠4,∠5是五边形ABCDE的外角,∠1=∠2=∠3=∠4=70°,则∠AED=100°.