题目内容
某一实验装置的截面图如图所示，上方装置可看做一长方形，其侧面与水平线的夹角为45°，下方是一个直径为70cm，高为100cm的圆柱形容器，若使容器中的液面与上方装置相接触，则容器中液体的高度至少应为（ ）| A、30cm | ||
| B、35cm | ||
C、35
| ||
| D、65cm |
考点：勾股定理的应用
专题：
分析：由题可知，进入容器中的三角形ABC可看作是一个斜边为40cm的等腰直角三角形，所以在此三角形中斜边上的高应该为20cm，因此若使高为55cm容器中的水面与圆桶相接触，由此可以求出水深．
解答：
解：如图，∵圆桶放置的角度与水平线的夹角为45°，∠BCA=90°，
∴依题意得△ABC是一个斜边为70cm的等腰直角三角形，
∴此三角形中斜边上的高应该为35cm，
∴水深至少应为100-35=65cm．
故选D．
解：如图，∵圆桶放置的角度与水平线的夹角为45°，∠BCA=90°，∴依题意得△ABC是一个斜边为70cm的等腰直角三角形，
∴此三角形中斜边上的高应该为35cm，
∴水深至少应为100-35=65cm．
故选D．
点评：解此题的关键是把实际问题转化为数学问题，抽象到等腰直角三角形中，利用它的性质即可解答．
练习册系列答案
相关题目
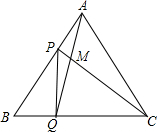如图，点P、Q分别是边长为4cm的等边△ABC边AB、BC上的动点，点P从顶点A，点Q从顶点B同时出发，且它们的速度都为1cm/s，下面四个结论：①BP=CM；②△ABQ≌△CAP；③∠CMQ的度数不变，始终等于60°；④当第