题目内容
11．观察下列运算过程：S=1+3+32+33+…+32012+32013①，①×3得3S=3+32+33+…+32013+32014②，②-①得2S=32014-1，$S=\frac{{{3^{2014}}-1}}{2}$．运用上面计算方法计算：1+5+52+53+…+52015+52016=$\frac{{5}^{2017}-1}{4}$．分析 设S=1+5+52+53+…+52015+52016，等式两边乘以5得到5S=5+52+53+…+52015+52017，然后把两式相减即可得到S的值．
解答 解：设S=1+5+52+53+…+52015+52016，
则5S=5+52+53+…+52015+52017，
所以4S=52017-1，
所以S=$\frac{{5}^{2017}-1}{4}$．
故答案为$\frac{{{5^{2017}}-1}}{4}$．
点评 本题考查了规律型-数字的变换类：认真观察、仔细思考，善用联想是解决这类问题的方法．
练习册系列答案
阅读快车系列答案
相关题目
如图，四个半径均为3cm的等圆依次外切，且∠O=90°，则图中阴影部分的面积为36cm2．
19．
如图，ABCD是⊙O内接矩形，半径r=2，AB=2，E，F分别是AC，CD上的动点，且AE=CF，则BE+BF的最小值是（ ）
如图，ABCD是⊙O内接矩形，半径r=2，AB=2，E，F分别是AC，CD上的动点，且AE=CF，则BE+BF的最小值是（ ）| A． | $\sqrt{7}$ | B． | 2$\sqrt{7}$ | C． | 3$\sqrt{3}$ | D． | 4$\sqrt{3}$ |
6．
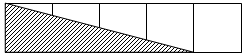如图，五个大小相同的小长方形拼在一起组成一个大长方形，那么图中阴影部分的面积是大长方形面积的（ ）
如图，五个大小相同的小长方形拼在一起组成一个大长方形，那么图中阴影部分的面积是大长方形面积的（ ）| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{5}$ | D． | $\frac{1}{5}$ |
17．下列几种说法中正确的是（ ）
| A． | 一个有理数的绝对值一定比0大 | |
| B． | 两个数比较大小，绝对值大的反而小 | |
| C． | 相反数等于它本身的数是0 | |
| D． | 若a＞0，b＜0且|a|＞|b|，则a+b＜0 |
如图，矩形ABCD中，AB=3，BC=4，点P在射线BC上运动，点P和点P′关于BD对称，当P′、P、D三点共线时运动停止，连接DP′、DP．设BP=x．