题目内容
10．如果要在一条直线上得到6条不同的线段，那么在这条直线上应选4个不同的点．分析 由于同一直线上的n个点之间有$\frac{n（n-1）}{2}$条线段，代入即可求得n的值．
解答 解：n个点之间有$\frac{n（n-1）}{2}$条线段，
$\frac{n（n-1）}{2}$=6，
解得n1=4，n2=-3（舍去），
则要得到6条不同的线段，在这条直线上应选4个不同点，
故答案为：4个．
点评 本题考查的是线段的条数的确定，掌握计算线段的公式$\frac{n（n-1）}{2}$（n是点的个数）是解题的关键．
练习册系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
如图，x所表示的点在数轴上的位置如图，则关于x的方程|x-3|+|6-x|=|5x|的解为x=$\frac{9}{7}$．
1．下列命题为真命题的是（ ）
| A． | 数轴上的每一个点都表示一个实数 | |
| B． | 如果两条直线被第三条直线所截，那么同旁内角互补 | |
| C． | 三角形的一个外角等于两个内角的和 | |
| D． | 估算$\sqrt{13.6}$的大小，如果结果精确到0.1，那么$\sqrt{13.6}$≈3.5 |
20．一次函数y=kx+b中的x，y的部分对应值如表：
根据表中数值分析以下四个结论：
①kb＜0；
②y的值随x值的增大而减小；
③方程kx+b=-9的解是x=3；
④当x＞-1时，y＞7．
其中一定正确的是（ ）
| x | … | -1 | 0 | 1 | 2 | … |
| y | … | 7 | 3 | -1 | -5 | … |
①kb＜0；
②y的值随x值的增大而减小；
③方程kx+b=-9的解是x=3；
④当x＞-1时，y＞7．
其中一定正确的是（ ）
| A． | ①②③ | B． | ②③④ | C． | ①③④ | D． | ①②④ |
的图象交开A（﹣2，1），B（1，a）两点．
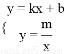的解．