题目内容
8. 如图,一架2.5米长的梯子AB斜靠在竖直的墙壁OC上,这时梯脚B到墙壁OC的距离为OB=0.7米,当梯子的顶端A沿墙壁下滑到达点A′时,点B沿水平地面向外滑动到B′点.
如图,一架2.5米长的梯子AB斜靠在竖直的墙壁OC上,这时梯脚B到墙壁OC的距离为OB=0.7米,当梯子的顶端A沿墙壁下滑到达点A′时,点B沿水平地面向外滑动到B′点.(1)当AA′=0.4米时,线段AA′的长度与线段BB′的长度相等吗?你是怎样知道的?
(2)能否存在一个点A′,使AA′=BB′?若存在,求出点A′的位置;若不存在,说明理由.
分析 (1)线段AA′的长度与线段BB′的长度不相等.在Rt△AOB中,利用勾股定理求出OA,在Rt△A′OB′中,利用勾股定理求出OB′,根据BB′=OB′-OB即可解决问题.
(2)设梯子顶端从A处下滑x米,点B向外也移动x米,根据勾股定理可得(x+0.7)2+(2.4-x)2=2.52,解方程即可.
解答 解:(1)线段AA′的长度与线段BB′的长度不相等.
理由:在Rt△AOB中,∵∠AOB=90°,AB=2.5,OB=0.7,
∴OA=$\sqrt{A{B}^{2}-O{B}^{2}}$=$\sqrt{2.{5}^{2}-0.{7}^{2}}$=2.4,
∵AA′=0.4,
∴OA′=OA-AA′=2,
在Rt△A′OB′中,∵∠A′OB′=90°,OA′=2,A′B′=2.5,
∴OB′=$\sqrt{A′B{′}^{2}-OB{′}^{2}}$=$\sqrt{2.{5}^{2}-{2}^{2}}$=1.5,
∴BB′=OB′-OB=1.5-0.7=0.8,
∴线段AA′的长度与线段BB′的长度不相等.
(2)存在.
设梯子顶端从A处下滑x米,点B向外也移动x米,
则有(x+0.7)2+(2.4-x)2=2.52,
解得:x1=1.7或x2=0(舍).
所以当梯子顶端从A处下滑1.7米时,点B向外也移动1.7米,即梯子顶端从A处沿墙AC下滑的距离与点B向外移动的距离有可能相等.
此时AA′=1.7米.
点评 本题考查了勾股定理在实际生活中的应用,本题中根据梯子长不会变的等量关系求解是解题的关键,属于中考常考题型.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图,长2.5米的梯子AB靠在墙上,梯子的底端A到墙根O的距离为0.7米,若梯子的底端B向下滑动0.4米′,那么梯子的下端A向外滑动( )
如图,长2.5米的梯子AB靠在墙上,梯子的底端A到墙根O的距离为0.7米,若梯子的底端B向下滑动0.4米′,那么梯子的下端A向外滑动( )
 如图,长2.5米的梯子AB靠在墙上,梯子的底端A到墙根O的距离为0.7米,若梯子的底端B向下滑动0.4米′,那么梯子的下端A向外滑动( )
如图,长2.5米的梯子AB靠在墙上,梯子的底端A到墙根O的距离为0.7米,若梯子的底端B向下滑动0.4米′,那么梯子的下端A向外滑动( )| A. | 0.4米 | B. | 0.7米 | C. | 0.8米 | D. | 不确定 |
13.不等式$\frac{1}{3}$(x-m)>3-m的解集为x>1,则m的值为( )
| A. | 1 | B. | -1 | C. | 4 | D. | -4 |
17. 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
 如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )
如图,在Rt△ACB中,∠C=90°,BE平分∠ABC,ED垂直平分AB于D,则图中的全等三角形对数共有( )| A. | 1对 | B. | 2对 | C. | 3对 | D. | 4对 |
18.南涧无量樱花谷的樱花在12月中旬左右盛开,花朵绚丽迷人,吸引了众多海内外游客,去年到樱花谷参观的游客约为150000人,将这个数据用科学记数法表示为( )
| A. | 1.5×103 | B. | 1.5×104 | C. | 0.15×105 | D. | 1.5×105 |
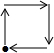
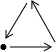
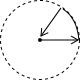
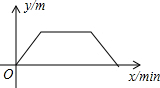 如图是王大爷早晨出门散步时,离家的距离y(m)与时间x(min)之间的变化关系,若用黑点表示王大爷家的位置,则王大爷散步行走的线路可能是( )
如图是王大爷早晨出门散步时,离家的距离y(m)与时间x(min)之间的变化关系,若用黑点表示王大爷家的位置,则王大爷散步行走的线路可能是( )

 如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).
如图,在平面直角坐标系中,四边形ABCD各顶点的坐标分别为A(0,1)、B(5,1)、C(7,3)、D(2,5).