题目内容
14.一个不透明的袋子里装着6个黄球,10个黑球和14个红球,他们除了颜色外完全相同.(1)小明和小颖玩摸球游戏,规定每人摸球一次再将球放回为依次游戏,若摸到黑球则小明获胜,摸到黄球则小颖获胜,这个游戏公平吗?说说你的理由.
(2)现在裁判向袋子中放入若干个红球,大量重复试验后,发现小明获胜的频率稳定在0.25附近,问裁判放入了多少个红球?
分析 (1)根据概率公式分别计算小明获胜和小颖获胜的概率,比较即可得;
(2)设向袋子中放入了x个红球,根据摸到黑球最终稳定的频率即为概率的估计值,列出方程求解可得.
解答 解:(1)不公平,
∵袋子中共有30个小球,从中摸出一个小球,是黑球的概率为$\frac{10}{30}$=$\frac{1}{3}$,
从中摸出一个小球,是黄球的概率为$\frac{6}{30}$=$\frac{1}{5}$,
∴这个游戏不公平;
(2)设裁判向袋子中放入了x个红球,
根据题意可得:$\frac{10}{30+x}$=0.25,
解得:x=10,
经检验:x=10是分式方程的解,
∴裁判放入了10个红球.
点评 本题主要考查概率公式和频率估计概率,熟练掌握概率公式:概率等于所求情况数与总情况数之比是解题的关键.

练习册系列答案
相关题目
 如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=$\frac{1}{3}$;若S△ABC=12,则S△ADF-S△BEF=2.
如图,△ABC中E是BC上的一点,EC=2BE,点D是AC的中点,则EF:AF=$\frac{1}{3}$;若S△ABC=12,则S△ADF-S△BEF=2. 如图,边长为3的正方形ABCD,以A为圆心,AB为半径作弧交DA的延长线于E,连接CE,则图中阴影部分面积为$\frac{9}{4}$π.
如图,边长为3的正方形ABCD,以A为圆心,AB为半径作弧交DA的延长线于E,连接CE,则图中阴影部分面积为$\frac{9}{4}$π.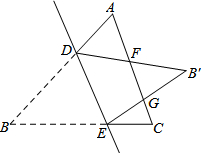 如图,已知△ABC中,AC=BC,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在B'处,DB'、EB'分别交AC于点F、G,若∠ADF=66°,则∠EGC的度数为66°.
如图,已知△ABC中,AC=BC,点D、E分别在边AB、BC上,把△BDE沿直线DE翻折,使点B落在B'处,DB'、EB'分别交AC于点F、G,若∠ADF=66°,则∠EGC的度数为66°.