题目内容
2. 如图,A、B、C为数轴(单位长度为1)上的三个点,其对应的数据都是整数,若点B对应的数比点A对应的数的2倍大7,那么点C对应的数是3.
如图,A、B、C为数轴(单位长度为1)上的三个点,其对应的数据都是整数,若点B对应的数比点A对应的数的2倍大7,那么点C对应的数是3.
分析 设点A对应的数为x,则点B对应的数为2x+7,由图可知,AB=3,即2x+7-x=3,解得:x=-4,则点B对应的数为-1,点C对应的数为-1+4=3.
解答 解:设点A对应的数为x,则点B对应的数为2x+7,
由图可知,AB=3,
即2x+7-x=3,
解得:x=-4,
则点B对应的数为-1,
点C对应的数为-1+4=3,
故答案为:3.
点评 本题考查了数轴,解决本题的关键是根据数轴得到AB=3,列出方程.

练习册系列答案
相关题目
12.在平面直角坐标系中,设点P到原点O的距离为ρ,OP与x轴正方向的夹角为α,则用[ρ,α]表示点P的极坐标,显然,点P的极坐标与它的坐标存在一一对应关系.例如:点P的坐标为(1,1),则其极坐标为[$\sqrt{2}$,45°].若点Q的极坐标为[4,120°],则点Q的坐标为( )
| A. | $(-\right.2,2\sqrt{3}\left.{\;})$ | B. | $(-2,-2\sqrt{3})$ | C. | (2$\sqrt{3}$,2) | D. | (2,2) |
13.己知菱形ABCD的边长是6,∠ADC=120°,点E在直线AD上,DE=3,连接BE与对角线AC相交于点M,则线段CM的长是4$\sqrt{3}$或$\frac{12\sqrt{3}}{5}$.
7.若数据8、4、x、2的平均数是4,则这组数据的中位数是( )
| A. | 2 | B. | 3 | C. | 4 | D. | 5 |
14. 如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
(1)计算上述试验中“4朝下”的频率是0.27;
(2)投掷一次正四面体,出现2朝下的概率是$\frac{1}{4}$;
(3)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
 如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:
如图,均匀的正四面体的各面依次标有1,2,3,4四个数字.小明做了60次投掷试验,结果统计如下:| 朝下数字 | 1 | 2 | 3 | 4 |
| 出现的次数 | 20 | 10 | 14 | 16 |
(2)投掷一次正四面体,出现2朝下的概率是$\frac{1}{4}$;
(3)随机投掷正四面体两次,请用列表或画树状图法,求两次朝下的数字之和大于4的概率.
12.矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6cm,则BD的长( )
| A. | 6cm | B. | 8cm | C. | 10cm | D. | 12cm |
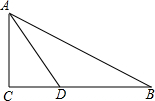 如图,△ABC中,∠C=90°,AD平分∠BAC,CD=$\frac{10}{3}$,BC=12,AB=13,则△ADB的面积是$\frac{65}{3}$.
如图,△ABC中,∠C=90°,AD平分∠BAC,CD=$\frac{10}{3}$,BC=12,AB=13,则△ADB的面积是$\frac{65}{3}$. 如图所示,以AB为对称轴,画出已知图形△CDE的轴对称图形.
如图所示,以AB为对称轴,画出已知图形△CDE的轴对称图形.