题目内容
15. 如图,AB是⊙O的直径,$\widehat{AD}$=$\widehat{DE}$,且AB=5,BD=4,求弦DE的长.
如图,AB是⊙O的直径,$\widehat{AD}$=$\widehat{DE}$,且AB=5,BD=4,求弦DE的长.
分析 连接AD,在Rt△ABD中利用勾股定理求出AD,根据等弧对等弦得出AD=DE.
解答  解:连接AD,
解:连接AD,
∵$\widehat{AD}$=$\widehat{DE}$,
∴AD=DE,
又∵AB为直径,
∴∠ADB=90°,
∵AB=5,BD=4,
∴DE=AD=$\sqrt{A{B}^{2}-B{D}^{2}}$=3,
∴DE的长为3.
点评 本题考查了圆周角定理,解答本题的关键是作出辅助线,求出AD的长度,难度一般.

练习册系列答案
相关题目
6.对于一次函数y=-2x+4,下列结论错误的是( )
| A. | 函数值随自变量的增大而减小 | |
| B. | 函数的图象不经过第三象限 | |
| C. | 函数的图象与x轴的交点坐标是(0,4) | |
| D. | 函数的图象向下平移4个单位长度得y=-2x的图象 |
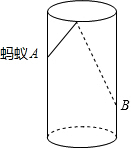 如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是13cm.
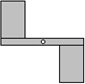
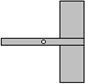
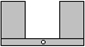
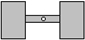
如图,透明的圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁,且离容器上沿3cm的点A处,则蚂蚁吃到饭粒需爬行的最短路径是13cm. 风车不能做成轴对称图形,应做成中心对称图形才能在风口处平稳旋转,如图,现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车,正确的粘合方法是( )
风车不能做成轴对称图形,应做成中心对称图形才能在风口处平稳旋转,如图,现有一长条矩形硬纸板(其中心有一个小孔)和两张全等的矩形薄纸片,将纸片粘到硬纸板上,做成一个能绕着小孔平稳旋转的风车,正确的粘合方法是( )