题目内容
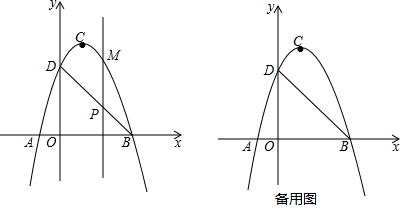
14. 直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )
直线a∥b,Rt△ABC的直角顶点C在直线a上,若∠1=35°,则∠2等于( )| A. | 65° | B. | 50° | C. | 55° | D. | 60° |
分析 先根据直角为90°,即可得到∠3的度数,再根据平行线的性质,即可得出∠2的度数.
解答  解:∵Rt△ABC的直角顶点C在直线a上,∠1=35°,
解:∵Rt△ABC的直角顶点C在直线a上,∠1=35°,
∴∠3=90°-35°=55°,
又∵a∥b,
∴∠2=∠3=55°,
故选:C.
点评 本题主要考查了平行线的性质,解题时注意:两直线平行同位角相等.

练习册系列答案
相关题目
5.化简:|-15|等于( )
| A. | 15 | B. | -15 | C. | ±15 | D. | $\frac{1}{15}$ |
17.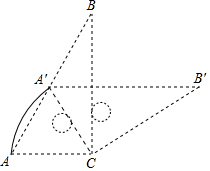 如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
 如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )
如图,△ABC和△A′B′C是两个完全重合的直角三角板,∠B=30°,斜边长为12cm.三角板A′B′C绕直角顶点C顺时针旋转,当点A′落在AB边上时,则点A′所转过的路径长为( )| A. | πcm | B. | 2πcm | C. | $\frac{8π}{3}cm$ | D. | 4πcm |
 解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.
解不等式组$\left\{\begin{array}{l}{5x+1>3(x-1)}\\{\frac{1}{2}x-1≤7-\frac{3}{2}x}\end{array}\right.$,并把它的解集在数轴上表示出来.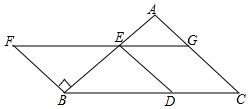 如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.
如图,以BC为底边的等腰△ABC,点D,E,G分别在BC,AB,AC上,且EG∥BC,DE∥AC,延长GE至点F,使得BE=BF.