题目内容
 已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)
已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3) =
= -1;(4)AE=2DE.其中错误结论的个数是
-1;(4)AE=2DE.其中错误结论的个数是
- A.0个
- B.1个
- C.2个
- D.3个
B
分析:(1)根据直径所对的圆周角是直角、等腰三角形的性质以及同弧所对的圆周角相等可求得∠EBC的度数;
(2)连接AD,由于AB=AC,∠ADB=90°,利用等腰三角形三线合一定理可知BD=CD;
(3)在等腰三角形ABC中,AB=AC;在等腰直角三角形ABE中,AB= AE,所以EC=
AE,所以EC= AE-AE=(
AE-AE=( -1)AE,从而求得
-1)AE,从而求得 的值;
的值;
(4)根据圆周角、弧、弦间的关系解答.
解答: 解:连接AD.
解:连接AD.
(1)∵AB是直径,
∴AD⊥BC;
又∵AB=AC,∠BAC=45°,
∴∠EAD= ∠BAC=22.5°;
∠BAC=22.5°;
而∠EBC=∠EAD(同弧所对的圆周角相等),
∴∠EBC=22.5°,
故本选项正确;
(2)∵AB是直径,
∴∠ADB=90°(直径所对的圆周角是直角);
又∵AB=AC,
∴BD=CD,
故本选项正确;
(3)在等腰直角三角形ABE中,AB= AE,
AE,
∴EC= AE-AE=(
AE-AE=( -1)AE,
-1)AE,
∴ =
= -1;
-1;
故本选项正确;
(4)∵∠ADE=∠ABE=45°(同弧所对的圆周角相等),∠DAE=∠DBE=22.5°(由(1)知),
∴∠ADE=2∠DAE,
∴ =2
=2 ,
,
故本选项错误.
综上所述,其中错误的结论有1个.
故选B.
点评:本题考查了圆周角定理、等腰直角三角形的判定和性质、等腰三角形三线合一定理,解题的关键是求出相应角的度数.
分析:(1)根据直径所对的圆周角是直角、等腰三角形的性质以及同弧所对的圆周角相等可求得∠EBC的度数;
(2)连接AD,由于AB=AC,∠ADB=90°,利用等腰三角形三线合一定理可知BD=CD;
(3)在等腰三角形ABC中,AB=AC;在等腰直角三角形ABE中,AB=
 AE,所以EC=
AE,所以EC= AE-AE=(
AE-AE=( -1)AE,从而求得
-1)AE,从而求得 的值;
的值;(4)根据圆周角、弧、弦间的关系解答.
解答:
 解:连接AD.
解:连接AD.(1)∵AB是直径,
∴AD⊥BC;
又∵AB=AC,∠BAC=45°,
∴∠EAD=
 ∠BAC=22.5°;
∠BAC=22.5°;而∠EBC=∠EAD(同弧所对的圆周角相等),
∴∠EBC=22.5°,
故本选项正确;
(2)∵AB是直径,
∴∠ADB=90°(直径所对的圆周角是直角);
又∵AB=AC,
∴BD=CD,
故本选项正确;
(3)在等腰直角三角形ABE中,AB=
 AE,
AE,∴EC=
 AE-AE=(
AE-AE=( -1)AE,
-1)AE,∴
 =
= -1;
-1;故本选项正确;
(4)∵∠ADE=∠ABE=45°(同弧所对的圆周角相等),∠DAE=∠DBE=22.5°(由(1)知),
∴∠ADE=2∠DAE,
∴
 =2
=2 ,
,故本选项错误.
综上所述,其中错误的结论有1个.
故选B.
点评:本题考查了圆周角定理、等腰直角三角形的判定和性质、等腰三角形三线合一定理,解题的关键是求出相应角的度数.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
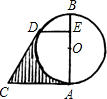 已知如图,AB是⊙O直径,∠C的两边分别与⊙O相切于A、D两点.DE⊥AB,垂足为E,AE=3,BE=1,则图中阴影部分面积( )
已知如图,AB是⊙O直径,∠C的两边分别与⊙O相切于A、D两点.DE⊥AB,垂足为E,AE=3,BE=1,则图中阴影部分面积( )A、4
| ||||||
B、
| ||||||
C、
| ||||||
D、4
|
 6、已知如图,AB是⊙O的直径,弦CD⊥AB于E,CD=6,AE=1,则⊙O的直径为( )
6、已知如图,AB是⊙O的直径,弦CD⊥AB于E,CD=6,AE=1,则⊙O的直径为( ) 19、已知如图,AB是⊙O的直径,AB垂直弦CD于点E,则在不添加辅助线的情况下,图中与∠CDB相等的角是
19、已知如图,AB是⊙O的直径,AB垂直弦CD于点E,则在不添加辅助线的情况下,图中与∠CDB相等的角是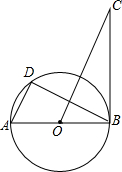 已知如图,AB是⊙O的直径,BC⊥AB于B,D是⊙O上的一点,且AD∥OC.
已知如图,AB是⊙O的直径,BC⊥AB于B,D是⊙O上的一点,且AD∥OC. 已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)
已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)