题目内容
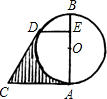 已知如图,AB是⊙O直径,∠C的两边分别与⊙O相切于A、D两点.DE⊥AB,垂足为E,AE=3,BE=1,则图中阴影部分面积( )
已知如图,AB是⊙O直径,∠C的两边分别与⊙O相切于A、D两点.DE⊥AB,垂足为E,AE=3,BE=1,则图中阴影部分面积( )A、4
| ||||||
B、
| ||||||
C、
| ||||||
D、4
|
分析:连OD,过D作DF⊥AC于F,由AE=3,BE=1,得到半径OA=OD=2,则OE=3-2=1;在Rt△ODE中,得到∠ODE=30°,则∠DOE=60°,DE=
OE=
,所以∠DOA=120°.再根据切线的性质得到∠CAE=∠CDO=90°,则∠C=180°-∠DOA=60°,在Rt△CDF中,∠CDF=90°-60°=30°,可求出CF,最后根据扇形的面积公式,利用S阴影部分=S梯形AEDC-S△ODE-S扇形ODA进行计算即可.
| 3 |
| 3 |
解答: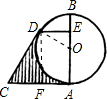 解:连OD,过D作DF⊥AC于F,如图,
解:连OD,过D作DF⊥AC于F,如图,
∵AE=3,BE=1,
∴AB=4,
∴OA=OD=2,OE=3-2=1,
在Rt△ODE中,OD=2OE,
∴∠ODE=30°,
∴∠DOE=60°,DE=
OE=
,
∴∠DOA=120°,
又∵CD,CA为⊙O的切线,
∴∠CAE=∠CDO=90°,
∴∠C=180°-∠DOA=60°,
而DF=EA=3,
在Rt△CDF中,∠CDF=90°-60°=30°,
∴CF=
=
,
∴S阴影部分=S梯形AEDC-S△ODE-S扇形ODA=
(
+2
)•3-
•
•1-
=4
-
π.
故选D.
 解:连OD,过D作DF⊥AC于F,如图,
解:连OD,过D作DF⊥AC于F,如图,∵AE=3,BE=1,
∴AB=4,
∴OA=OD=2,OE=3-2=1,
在Rt△ODE中,OD=2OE,
∴∠ODE=30°,
∴∠DOE=60°,DE=
| 3 |
| 3 |
∴∠DOA=120°,
又∵CD,CA为⊙O的切线,
∴∠CAE=∠CDO=90°,
∴∠C=180°-∠DOA=60°,
而DF=EA=3,
在Rt△CDF中,∠CDF=90°-60°=30°,
∴CF=
| DF | ||
|
| 3 |
∴S阴影部分=S梯形AEDC-S△ODE-S扇形ODA=
| 1 |
| 2 |
| 3 |
| 3 |
| 1 |
| 2 |
| 3 |
| 120•π•22 |
| 360 |
=4
| 3 |
| 4 |
| 3 |
故选D.
点评:本题考查了扇形的面积公式:S=
;也考查了含30度的直角三角形三边的关系、切线的性质以及梯形的面积公式.
| n•π•R2 |
| 360 |

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 6、已知如图,AB是⊙O的直径,弦CD⊥AB于E,CD=6,AE=1,则⊙O的直径为( )
6、已知如图,AB是⊙O的直径,弦CD⊥AB于E,CD=6,AE=1,则⊙O的直径为( ) 19、已知如图,AB是⊙O的直径,AB垂直弦CD于点E,则在不添加辅助线的情况下,图中与∠CDB相等的角是
19、已知如图,AB是⊙O的直径,AB垂直弦CD于点E,则在不添加辅助线的情况下,图中与∠CDB相等的角是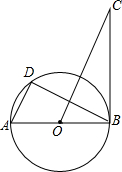 已知如图,AB是⊙O的直径,BC⊥AB于B,D是⊙O上的一点,且AD∥OC.
已知如图,AB是⊙O的直径,BC⊥AB于B,D是⊙O上的一点,且AD∥OC. 已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)
已知如图:AB是⊙O的直径,AB=AC,BC交⊙O于点D,AC交⊙O于点E,∠BAC=45°,给出以下四个结论:(1)∠EBC=22.5°(2)BD=DC;(3)