题目内容
19、已知如图，AB是⊙O的直径，AB垂直弦CD于点E，则在不添加辅助线的情况下，图中与∠CDB相等的角是∠BAC或∠DCB
（写出一个即可）．分析：根据垂径定理和圆周角定理可证∠CDB=∠BAC=∠DCB．
解答：解：∵AB是⊙O的直径，AB垂直弦CD于点E，
∴弧BD=弧BC，
∴∠CDB=∠BAC=∠DCB．
∴弧BD=弧BC，
∴∠CDB=∠BAC=∠DCB．
点评：此题综合考查了垂径定理：垂直于弦的直径平分线并且平分弦所在的弧．及圆周角定理：在同圆或等圆中，同弧或等弧所对的圆周角相等，都等于这条弧所对的圆心角的一半．
练习册系列答案
相关题目
6、已知如图，AB是⊙O的直径，弦CD⊥AB于E，CD=6，AE=1，则⊙O的直径为（ ）
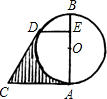已知如图，AB是⊙O直径，∠C的两边分别与⊙O相切于A、D两点．DE⊥AB，垂足为E，AE=3，BE=1，则图中阴影部分面积（ ）A、4
| ||||||
B、
| ||||||
C、
| ||||||
D、4
|
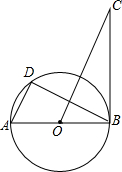已知如图，AB是⊙O的直径，BC⊥AB于B，D是⊙O上的一点，且AD∥OC．
已知如图：AB是⊙O的直径，AB=AC，BC交⊙O于点D，AC交⊙O于点E，∠BAC=45°，给出以下四个结论：（1）∠EBC=22.5°（2）BD=DC；（3）