题目内容
5.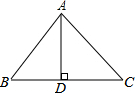 如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°,AC=3$\sqrt{2}$.
如图,在△ABC中,AD⊥BC,垂足为D,∠B=60°,∠C=45°,AC=3$\sqrt{2}$.(1)求AD的长;
(2)求△ABC的面积.
分析 (1)先根据勾股定理求出AD的长;
(2)由锐角三角函数的定义求出BD的长,再由三角形面积公式即可求得结论.
解答 解:(1)∵AD⊥BC,垂足为D,∠C=45°,AC=3$\sqrt{2}$,
∴△ADC是等腰直角三角形,AD=CD,
∴2AD2=AC2,即2AD2=(3$\sqrt{2}$)2,解得AD=3,
(2)∵∠B=60°,
∴BD=$\frac{AD}{tan60°}$=$\frac{3}{\sqrt{3}}$=$\sqrt{3}$,
∴BC=BD+CD=3+$\sqrt{3}$,
∴△ABC的面积=$\frac{1}{2}$BC•AD=$\frac{1}{2}$×3×(3+$\sqrt{3}$)=$\frac{9+3\sqrt{3}}{2}$.
点评 本题考查的是勾股定理,三角函数,三角形的面积,熟知在任何一个直角三角形中,两条直角边长的平方之和一定等于斜边长的平方是解答此题的关键.

练习册系列答案
相关题目
15.$\frac{1}{2}$,$\frac{1}{2}$,$\frac{1}{2}$,$\frac{7}{16}$,$\frac{11}{32}$,( )
| A. | $\frac{15}{64}$ | B. | $\frac{1}{4}$ | C. | $\frac{13}{48}$ | D. | $\frac{1}{3}$ |
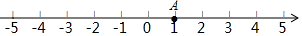 如图,在数轴上,点A表示的数是1,现将点A沿数轴做如下移动,第一次点A向左移动3 个单位长度到达点A1,点A1表示的数是-2;
如图,在数轴上,点A表示的数是1,现将点A沿数轴做如下移动,第一次点A向左移动3 个单位长度到达点A1,点A1表示的数是-2;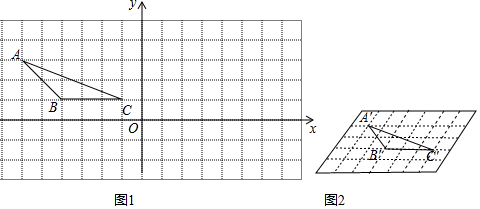
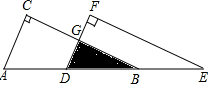 如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.
如图将Rt△ABC沿斜边AB向右平移5cm,得到Rt△DEF.已知AB=10cm,BC=8cm.求图中阴影部分三角形的周长.