题目内容
某商店以每件20元的价格购进一批商品,若每件商品售价a元,则每天可卖出(800-10a)件.如果商店计划要每天恰好盈利8000元,并且要使每天的销售量尽量大,求每件商品的售价是多少元.
考点:一元二次方程的应用
专题:销售问题
分析:根据利润=售价-进价列出方程,求出方程的解得到a的值,即可确定出要使每天的销售量尽量大时每件商品的售价.
解答:解:根据题意,得(a-20)(800-10a)=8000(20≤a≤80),
整理,得a2-100a+2400=0,即(a-40)(a-60)=0,
解得:a1=40,a2=60,
当a=40时,800-10a=800-10×40=800-400=400(件);
当a=60时,800-10a=800-10×60=800-600=200(件),
要使每天的销售量尽量大,故a=40,
答:商店计划要每天恰好盈利8000元,并且要使每天的销售量尽量大,每件商品的售价应是40元.
整理,得a2-100a+2400=0,即(a-40)(a-60)=0,
解得:a1=40,a2=60,
当a=40时,800-10a=800-10×40=800-400=400(件);
当a=60时,800-10a=800-10×60=800-600=200(件),
要使每天的销售量尽量大,故a=40,
答:商店计划要每天恰好盈利8000元,并且要使每天的销售量尽量大,每件商品的售价应是40元.
点评:此题考查了一元二次方程的应用,弄清题意是解本题的关键.

练习册系列答案
 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案 阳光同学一线名师全优好卷系列答案
阳光同学一线名师全优好卷系列答案
相关题目
对于一组数据2,4,4,5,3,9,4,5,1,8,其众数、中位数分别为( )
| A、4,2 | B、4,6 |
| C、4,4 | D、5,4 |
在-(-5),-(-5)2,-|-5|,(-5)3中正数有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
 如图,在⊙O中,弦AC与BD交于点E,AB=8,AE=6,ED=4,求CD的长.
如图,在⊙O中,弦AC与BD交于点E,AB=8,AE=6,ED=4,求CD的长.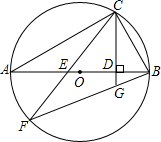 如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度.
如图,已知AB是⊙O的直径,点C是⊙O上一点,连接BC,过点C作直线CD⊥AB于点D,弦CF与AB交于点E,弦BF与直线CD交于点G.已知BG=2,GF=4,求:BC的长度.