Question

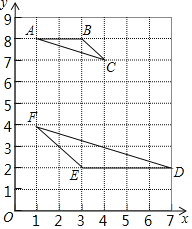
【题目】在如图平面直角坐标系中，矩形的顶点的坐标为，、分别落在轴和轴上，是矩形的对角线. 将绕点逆时针旋转，使点落在轴上，得到，与相交于点，反比例函数的图象经过点，交于点.

（1）求的值和点的坐标；

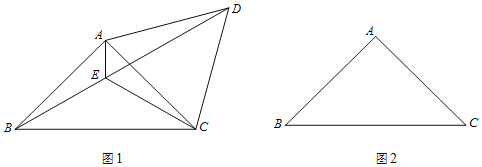
（2）连接，则图中是否存在与相似的三角形？若存在，请把它们一一找出来，并选其中一种进行证明；若不存在，请说明理由；

（3）在线段上存在这样的点，使得是等腰三角形，请直接写出点的坐标.

Answer 1

【答案】（1），G；（2），， ，证明见解析；（3） 或或

【解析】

（1）证明△COF∽△AOB，则，求得：点F的坐标为（1，2），即可求解；

（2）△COF∽△BFG；△AOB∽△BFG；△ODE∽△BFG；△CBO∽△BFG．证△OAB∽△BFG：，即可求解．

（3）分GF=PF、PF=PG、GF=PG三种情况，分别求解即可．

（1）∵四边形为矩形，点的坐标为，

∴，

∵是旋转得到的，即：，

∴，

∴，

∴，

∴，

∴，

∴点的坐标为，

∵的图象经过点，

∴，得，

∵点在上，

∴点的横坐标为4，

对于，当，得，

∴点的坐标为；

（2）；； ；．

下面对进行证明：

∵点的坐标为，

∴，

∵，

∴，

．

∴，．

∴，

∵，

∴．

（3）设点，而点、点，

则，，，

当时，即，解得： （舍去负值）；

当时，同理可得：；

当时，同理可得： （舍去正值）；

综上，点的坐标为或或．