题目内容
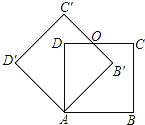
【题目】问题情境:如图1,直角三角板ABC中,∠C=90°,AC=BC,将一个用足够长的的细铁丝制作的直角的顶点D放在直角三角板ABC的斜边AB上,再将该直角绕点D旋转,并使其两边分别与三角板的AC边、BC边交于P、Q两点.
问题探究:(1)在旋转过程中,
①如图2,当AD=BD时,线段DP、DQ有何数量关系?并说明理由.
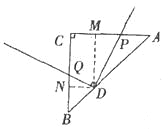
②如图3,当AD=2BD时,线段DP、DQ有何数量关系?并说明理由.
③根据你对①、②的探究结果,试写出当AD=nBD时,DP、DQ满足的数量关系为_______________(直接写出结论,不必证明)
(2)当AD=BD时,若AB=20,连接PQ,设△DPQ的面积为S,在旋转过程中,S是否存在最小值或最大值?若存在,求出最小值或最大值;若不存在,请说明理由.

图1 图2 图3
【答案】(1)① DP=DQ,理由见解析; ②DP=2DQ,理由见解析; ③DP=nDQ;(2)S有最小值为25; S有最大值为10,理由见解析.
【解析】
(1)①首先利用等腰直角三角形的性质得出△ADP≌△CDQ(ASA),即可得出答案;
②首先得出△DPM∽△DQN,则![]() ,求出△AMD∽△BND,进而得出答案.
,求出△AMD∽△BND,进而得出答案.
③根据已知得出Rt△DNP∽Rt△DMQ,则![]() ,则AD=nBD,求出即可;
,则AD=nBD,求出即可;
(2)当DP⊥AC时,x最小,最小值是5![]() .此时,S有最小值;当点P与点A重合时,x最大,最大值为10,分别求出即可.
.此时,S有最小值;当点P与点A重合时,x最大,最大值为10,分别求出即可.
解:(1)①DP=DQ
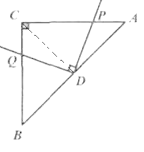
理由:连接CD,
∵AD=BD,△ABC是等腰直角三角形,
∴AD=CD,∠A=∠DCQ,∠ADC=90°,∴∠ADP+∠PDC=∠CDQ+∠PDC=90°,
∴∠ADP=∠CDQ,∴△ADP≌△CDQ,∴DP=DQ.
② DP=" 2DQ" .
理由:如图,过点D作DM⊥AC、DN⊥BC,垂足分别为M、N,
∴∠DMP=∠DNQ=90°,∠MDP=∠NDQ,
∴△DPM∽△DQN,∴DM:DN="DP:DQ" .
∵∠AMD=∠DNB=90°,∠A=∠B,
∴△AMD∽△BND,∴AD:BD=DM:DN.
∴DP:DQ=AD:BD=2BD:BD=2:1,
∴DP=2DQ.
③DP=NQ.
(2)存在,设DQ=x,由(1)①知DP=x,
∴S=![]()
![]() ,
,
当DP⊥AC时,x最小,最小值是![]() ,此时,S有最小值,
,此时,S有最小值,![]()
当点P与点A重合时,x最大,最大值是10,此时,S有最大值,![]()

 口算能手系列答案
口算能手系列答案【题目】如图,在![]() 中,直径
中,直径![]() 垂直于不过圆心
垂直于不过圆心![]() 的弦
的弦![]() ,垂足为点
,垂足为点![]() ,连接
,连接![]() ,
,![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .过点
.过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() ,点
,点![]() 为
为![]() 上一动点,设线段
上一动点,设线段![]() 的长为
的长为![]() .
.
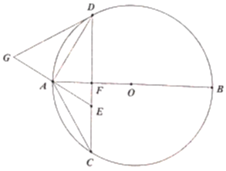
(1)求证:![]() ;
;
(2)求证:![]() ;
;
(3)设![]() 半径为
半径为![]() ,若点
,若点![]() 为
为![]() 中点,求
中点,求![]() 的取值范围.
的取值范围.
【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为连续接球10个,每垫球到位1个记1分.
运动员甲测试成绩表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 | 7 | 7 | 5 | 8 | 7 | 8 | 7 |
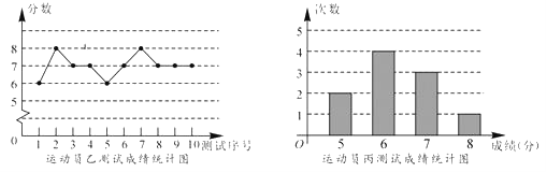
(1)写出运动员甲测试成绩的众数和中位数;
(2)在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?为什么?(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)