题目内容
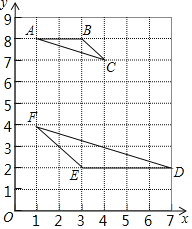
【题目】如图,在平面直角坐标系中,每个小方格都是边长为1个单位的小正方形,点A、B、C都是格点![]() 每个小方格的顶点叫格点
每个小方格的顶点叫格点![]() ,其中
,其中![]() ,
,![]() ,
,![]() .
.
![]() 外接圆的圆心坐标是______;
外接圆的圆心坐标是______;
![]() 外接圆的半径是______;
外接圆的半径是______;
![]() 已知
已知![]() 与
与![]() 点D、E、F都是格点
点D、E、F都是格点![]() 成位似图形,则位似中心M的坐标是______;
成位似图形,则位似中心M的坐标是______;
![]() 请在网格图中的空白处画一个格点
请在网格图中的空白处画一个格点![]() ,使
,使![]() ∽
∽![]() ,且相似比为
,且相似比为![]() :1.
:1.
【答案】(1)(2,6);(2)![]() ; (3)(3,6) ;(4)见解析.
; (3)(3,6) ;(4)见解析.
【解析】
(1)根据作图,结合网格特点解答;
(2)根据线段垂直平分线的性质和三角形的外接圆的概念解答;
(3)根据位似变换和位似中心的概念解答;
(4)根据相似三角形的对应边的比相等,都等于相似比解答.
解:(1)如图1,
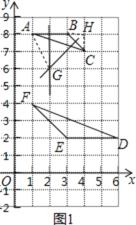
由作图可知△ABC外接圆的圆心坐标是(2,6),
故答案为:(2,6);
(2)作AB、BC的垂直平分线交于G,连接AG,
根据网格特点可知,点G的坐标为(2,6),
则AG=![]() =
=![]() ,
,
则△ABC外接圆的半径是![]() ,
,
故答案为:![]() ;
;
(3)如图2,连接BE、FC,
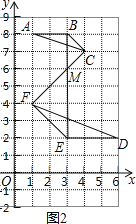
根据网格特点,BE与FC交于点M,
点M的坐标为(3,6),
根据位似中心的概念可知,位似中心M的坐标是(3,6),
故答案为:(3,6);
(4)由网格特点可知,AB=2,BC=![]() ,AC=
,AC=![]() ,
,
∵△A1B1C1∽△ABC,且相似比为![]() :1,
:1,
∴A1B1=2![]() ,B1C1=2,A1C1=2
,B1C1=2,A1C1=2![]() ,
,
所求的△A1B1C1如图3.

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案
相关题目