题目内容
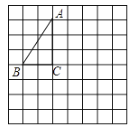
【题目】在每个小正方形的边长为1的网格中，点
，
，
均在格点上，点
，
分别为线段
，
上的动点．
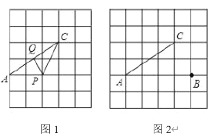
(I)如图(1)，当点，分别为，中点时，
的值为__________；
(Ⅱ)当取得最小值时，在如图(2)所示的网格中，用无刻度的真尺，画出线段
，
，简要说明点和点的位置是如何找到的(不要求证明)__________．
【答案】
取格点
，
， 连接
交
于点
，交
于点
【解析】
(I)根据勾股定理求出PC、BC的长，再根据三角形的中位线定理求出PQ的长，即可解答；
(Ⅱ)连接EF交AB于点P，画出图形解答即可．
(I)如图：连接BC
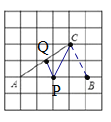
根据勾股定理可求得：PC=
,
BC=，
∵，分别为，中点，
∴
∴PC+PQ的值；
故答案为：；
(Ⅱ)如图所示，取格点E，F，连接EF交AB于点P，交AC于点Q．
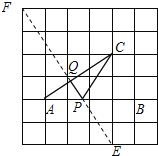
此时，PC+PQ最短．（PC+PQ=PE+PQ，根据垂线段最短，可知当EF⊥AC时，PE+PQ最短），
故答案为：取格点E，F，连接EF交AB于点P，交AC于点Q
练习册系列答案
相关题目
