ЬтФПФкШн
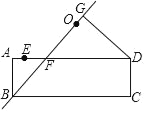
ЁОЬтФПЁПЁїABCЪЧЕШБпШ§НЧаЮЃЌЕуDЪЧЩфЯпBCЩЯЕФвЛИіЖЏЕуЃЈЕуDВЛгыЕуBЁЂCжиКЯЃЉЃЌЁїADEЪЧвдADЮЊБпЕФЕШБпШ§НЧаЮЃЌЙ§ЕуEзїBCЕФЦНааЯпЃЌЗжБ№НЛЩфЯпABЁЂACгкЕуFЁЂGЃЌСЌНгBEЃЎ
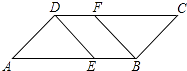
ЃЈ1ЃЉШчЭМЃЈaЃЉЫљЪОЃЌЕБЕуDдкЯпЖЮBCЩЯЪБЃЎ
ЂйЧѓжЄЃКЁїAEBЁеЁїADCЃЛ
ЂкЬНОПЫФБпаЮBCGEЪЧдѕбљЬиЪтЕФЫФБпаЮЃПВЂЫЕУїРэгЩЃЛ
ЃЈ2ЃЉШчЭМЃЈbЃЉЫљЪОЃЌЕБЕуDдкBCЕФбгГЄЯпЩЯЪБЃЌжБНгаДГіЃЈ1ЃЉжаЕФСНИіНсТлЪЧЗёГЩСЂЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЧщПіЯТЃЌЕБЕуDдЫЖЏЕНЪВУДЮЛжУЪБЃЌЫФБпаЮBCGEЪЧСтаЮЃПВЂЫЕУїРэгЩЃЎ
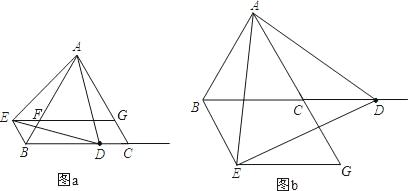
ЁОД№АИЁПЃЈ1ЃЉЂйМћНтЮіЃЌЂкЫФБпаЮBCGEЪЧЦНааЫФБпаЮЃЌМћНтЮіЃЛЃЈ2ЃЉЂйЂкЖМГЩСЂЃЛЃЈ3ЃЉЕБCDЃНCB ЃЈЁЯCADЃН30ЁуЛђЁЯBADЃН90ЁуЛђЁЯADCЃН30ЁуЃЉЪБЃЌЫФБпаЮBCGEЪЧСтаЮЃЌМћНтЮі.
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЕШБпШ§НЧаЮЕФаджЪПЩЕУABЃНACЃЌAEЃНADЃЌЁЯBACЃНЁЯEADЃН60ЁуЃЌШЛКѓЧѓГіЁЯBAEЃНЁЯCADЃЌдйРћгУЁАБпНЧБпЁБжЄУїЁїAEBКЭЁїADCШЋЕШЃЛЂкЫФБпаЮBCGEЪЧЦНааЫФБпаЮЃЌвђЮЊЁїAEBЁеЁїADCЃЌЫљвдПЩЕУЁЯABEЃНЁЯCЃН60ЁуЃЌНјЖјжЄУїЁЯABEЃНЁЯBACЃЌдђПЩЕУЕНEBЁЮGCгжEGЁЮBCЃЌЫљвдЫФБпаЮBCGEЪЧЦНааЫФБпаЮЃЛ
ЃЈ2ЃЉИљОнЃЈ1ЃЉЕФЫМТЗНтД№МДПЩЃЎЃЈ3ЃЉЕБCDЃНCBЪБЃЌЫФБпаЮBCGEЪЧСтаЮЃЌгЩЃЈ1ЃЉПЩжЊЁїAEBЁеЁїADCЃЌПЩЕУBEЃНCDЃЌдйжЄУїBEЃНCBЃЌМДСкБпЯрЕШЕФЦНааЫФБпаЮЪЧСтаЮЃЎ
жЄУїЃКЃЈ1ЃЉЂйЁпЁїABCКЭЁїADEЖМЪЧЕШБпШ§НЧаЮЃЌ
ЁрAEЃНADЃЌABЃНACЃЌЁЯEADЃНЁЯBACЃН60ЁуЃЎ
гжЁпЁЯEABЃНЁЯEADЉЁЯBADЃЌЁЯDACЃНЁЯBACЉЁЯBADЃЌ
ЁрЁЯEABЃНЁЯDACЃЌ
ЁрЁїAEBЁеЁїADCЃЈSASЃЉЃЎ
ЂкЗНЗЈвЛЃКгЩЂйЕУЁїAEBЁеЁїADCЃЌ
ЁрЁЯABEЃНЁЯCЃН60ЁуЃЎ
гжЁпЁЯBACЃНЁЯCЃН60ЁуЃЌ
ЁрЁЯABEЃНЁЯBACЃЌ
ЁрEBЁЮGCЃЎ
гжЁпEGЁЮBCЃЌ
ЁрЫФБпаЮBCGEЪЧЦНааЫФБпаЮЃЎ
ЗНЗЈЖўЃКжЄГіЁїAEGЁеЁїADBЃЌЕУEGЃНABЃНBCЃЎ
ЁпEGЁЮBCЃЌ
ЁрЫФБпаЮBCGEЪЧЦНааЫФБпаЮЃЎ
ЃЈ2ЃЉЂйЂкЖМГЩСЂЃЎ
ЃЈ3ЃЉЕБCDЃНCB ЃЈЁЯCADЃН30ЁуЛђЁЯBADЃН90ЁуЛђЁЯADCЃН30ЁуЃЉЪБЃЌЫФБпаЮBCGEЪЧСтаЮЃЎ
РэгЩЃКЗНЗЈвЛЃКгЩЂйЕУЁїAEBЁеЁїADCЃЌ
ЁрBEЃНCD
гжЁпCDЃНCBЃЌ
ЁрBEЃНCBЃЎ
гЩЂкЕУЫФБпаЮBCGEЪЧЦНааЫФБпаЮЃЌ
ЁрЫФБпаЮBCGEЪЧСтаЮЃЎ
ЗНЗЈЖўЃКгЩЂйЕУЁїAEBЁеЁїADCЃЌ
ЁрBEЃНCDЃЎ
гжЁпЫФБпаЮBCGEЪЧСтаЮЃЌ
ЁрBEЃНCB
ЁрCDЃНCBЃЎ
ЗНЗЈШ§ЃКЁпЫФБпаЮBCGEЪЧЦНааЫФБпаЮЃЌ
ЁрBEЁЮCGЃЌEGЁЮBCЃЌ
ЁрЁЯFBEЃНЁЯBACЃН60ЁуЃЌЁЯFЃНЁЯABCЃН60Ёу
ЁрЁЯFЃНЁЯFBEЃН60ЁуЃЌЁрЁїBEFЪЧЕШБпШ§НЧаЮЃЎ
гжЁпABЃНBCЃЌЫФБпаЮBCGEЪЧСтаЮЃЌ
ЁрABЃНBEЃНBFЃЌ
ЁрAEЁЭFG
ЁрЁЯEAGЃН30ЁуЃЌ
ЁпЁЯEADЃН60ЁуЃЌ
ЁрЁЯCADЃН30ЁуЃЎ