题目内容
19. 如图某防汛大堤的横断面为梯形ABCD,斜坡AB的坡度i1=1:1.5,斜坡CD的坡度i2=1:1,大堤顶高AD为10米,为了增强抗洪能力,现将大堤加高,加高部分的横截面为梯形ADFE,AD∥EF,且点E、F分别在BA、CD的延长线上,新坝顶宽EF为7.5米,求大堤加高了多少米?
如图某防汛大堤的横断面为梯形ABCD,斜坡AB的坡度i1=1:1.5,斜坡CD的坡度i2=1:1,大堤顶高AD为10米,为了增强抗洪能力,现将大堤加高,加高部分的横截面为梯形ADFE,AD∥EF,且点E、F分别在BA、CD的延长线上,新坝顶宽EF为7.5米,求大堤加高了多少米?
分析 分别过E、F作AD的垂线,设垂足为G、H;可设大坝加高了xm,在Rt△AEG和Rt△FHD中,分别用坡面的铅直高x和坡比表示出各自的水平宽,即AG、DH的长,进而可表示出AD的长,已知了DC长7.5m,由此可列出关于x的方程,即可求出大堤加高的高度.
解答  解:作EG⊥AD,FH⊥AD,G、H分别为垂足,
解:作EG⊥AD,FH⊥AD,G、H分别为垂足,
∵EF∥AD,
∴∠EGH=∠FHG=∠EFH=90°,
∴四边形EFHG是矩形;
∴GH=EF=7.5,
设大堤加高xm,
则EG=FH=xm,
∵i1=$\frac{EG}{AG}$=$\frac{1}{1.5}$,i2=$\frac{FH}{DH}$=$\frac{1}{1}$,
∴AG=1.5xm,DC=1xm,
∵AG+GH+HD=AD=10m,
∴1.5x+7.5+x=10,
解得:x=1.
∴大堤加高了1m.
点评 此题考查了坡度坡角问题.注意添加辅助线,构造出直角三角形并借助于直角三角形的性质求解,注意数形结合思想与方程思想的应用.

练习册系列答案
相关题目
7.若一批校服按七折出售,每件为x元,则这批校服每件的原价为( )
| A. | x•70% | B. | $\frac{x}{70%}$ | C. | x•30% | D. | $\frac{x}{30%}$ |
17. 如图,将△AOB绕点O逆时针方向旋转45°后得到△A′OB′,若∠AOB=10°,则∠AOB′的度数是( )
如图,将△AOB绕点O逆时针方向旋转45°后得到△A′OB′,若∠AOB=10°,则∠AOB′的度数是( )
 如图,将△AOB绕点O逆时针方向旋转45°后得到△A′OB′,若∠AOB=10°,则∠AOB′的度数是( )
如图,将△AOB绕点O逆时针方向旋转45°后得到△A′OB′,若∠AOB=10°,则∠AOB′的度数是( )| A. | 25° | B. | 30° | C. | 35° | D. | 40° |
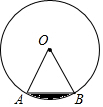 如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积.
如图,在半径为6的⊙O中,弦AB长为6.求弦AB与$\widehat{AB}$所围成的阴影部分的面积.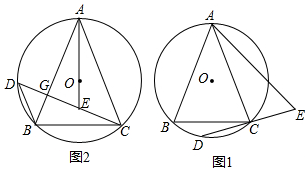
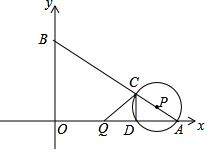 如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.
如图,在平面直角坐标系中,O为坐标原点,点A、B的坐标分别为(8,0)、(0,6).动点Q从点O、动点P从点A同时出发,分别沿着OA方向、AB方向均以1个单位长度/秒的速度匀速运动,运动时间为t(秒)(0<t≤5).以P为圆心,PA长为半径的⊙P与AB、OA的另一个交点分别为点C、D,连结CD、QC.