Question

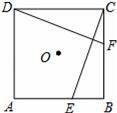
如图，E、F分别是正方形ABCD的边AB、BC上的点，BE=CF，连接CE、DF．△CDF可以看作是将△BCE绕正方形ABCD的中心O按逆时针方向旋转得到．则旋转的角度为　　°．

Answer 1

90【考点】旋转的性质；正方形的性质．

【分析】根据旋转性质得出旋转后C到D，只要根据正方形的性质和三角形的内角和定理求出∠COD即可．

【解答】解：将△CBE绕正方形的对角线交点O按顺时针方向旋转到△CDF时，C和D重合，

即∠COD是旋转角，

∵四边形ABCD是正方形，

∴∠OCD=∠ODC=45°，

∴∠COD=180°﹣45°﹣45°=90°，

即旋转角是90°，

故答案为90．