题目内容
如图,在▱ABCD中,点E、F是AD、BC的中点,连接BE、DF.
(1)求证:BE=DF.
(2)若BE平分∠ABC且交边AD于点E,如果AB=6cm,BC=10cm,试求线段DE的长.
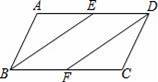

【考点】平行四边形的判定与性质.
【分析】(1)由四边形ABCD是平行四边形,可得AD∥BC,AD=BC,又由点E、F分别是▱ABCD边AD、BC的中点,可得DE=BF,证得四边形BFDE是平行四边形,即可证得结论.
(2)由平行线的性质和角平分线得出∠ABE=∠AEB,证出AE=AB=6cm,即可得出结果.
【解答】(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC,AD=BC,
∵点E、F分别是▱ABCD边AD、BC的中点,
∴DE=
 AD,BF=
AD,BF=
 BC,
BC,
∴DE=BF,
∴四边形BFDE是平行四边形,
∴BE=DF.
(2)解:∵AD∥BC,
∴∠AEB=∠CBE,
∵BE平分∠ABC,
∴∠ABE=∠CBE,
∴∠ABE=∠AEB,
∴AE=AB=6cm,
∴DE=AD﹣AE=10cm﹣6cm=4cm.

练习册系列答案
相关题目
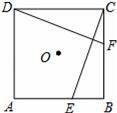
 ⊥AB于G,猜想CD与AB的位置关系,并说明理由.
⊥AB于G,猜想CD与AB的位置关系,并说明理由.
 .
.  果正确的是()
果正确的是()
 ﹣
﹣

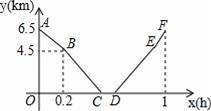

 与
与 在同一直角坐标系下的图象大致是( ).
在同一直角坐标系下的图象大致是( ).