题目内容
2.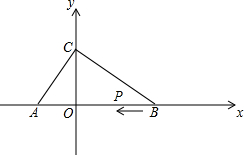 如图,在平面直角坐标系中,A(-1,0),B(3,0),C(0,2)
如图,在平面直角坐标系中,A(-1,0),B(3,0),C(0,2)(1)求△ABC的面积;
(2)若点P从B点出发沿射线BA的方向匀速移动,速度为1个单位/秒,设移动时间为t秒,当t为何值时,△PAC的面积等于△BOC的面积.
分析 (1)根据已知点的坐标来求线段AB,OC的长度,然后由三角形的面积公式进行解答;
(2)分类讨论:点P在点A的右边和左边两种情况,由三角形的面积公式解答.
解答 解:(1)∵A(-1,0),B(3,0),C(0,2),
∴AB=4,OC=2,
∴S△ABC=$\frac{1}{2}$AB•OC=$\frac{1}{2}$×4×2=4,即△ABC的面积是4;
(2)$\frac{1}{2}$AP•OC=$\frac{1}{2}$OB•OC,即AP=OB=3.
当点P在点A的右边时,AP=3,则BP=4-3=1,所以t=1;
当点P在点A的左边时,AP=3,则BP=4+3=7,所以t=7;
综上所述,当t为1或7时,△PAC的面积等于△BOC的面积.
点评 本题考查了三角形的面积和坐标与图形性质.熟知三角形的面积公式是解题的关键.

练习册系列答案
 天天练口算系列答案
天天练口算系列答案
相关题目
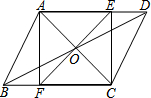 如图,在?ABCD中,对角线AC、BD相交于点O,直线EF经过点O,交AD于E,交BC于F,且AF⊥BC
如图,在?ABCD中,对角线AC、BD相交于点O,直线EF经过点O,交AD于E,交BC于F,且AF⊥BC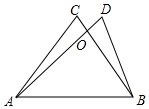 如图,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8cm,AD=10cm,OD=OC=2cm,求OB的长.
如图,△AOC≌△BOD,∠C与∠D是对应角,AC与BD是对应边,AC=8cm,AD=10cm,OD=OC=2cm,求OB的长.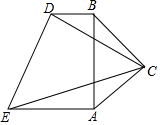 如图,在梯形AEDB中,BD∥AE,∠ABD=90°,在AB的右侧作Rt△ACB,∠ACB=90°,AC=BC,且∠ECD=45°
如图,在梯形AEDB中,BD∥AE,∠ABD=90°,在AB的右侧作Rt△ACB,∠ACB=90°,AC=BC,且∠ECD=45°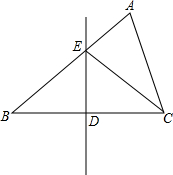 如图,在△ABC中,∠A=60°,边BC的垂直平分线分别交AB,BC于点E,D,连接EC.若∠B=∠ACE,求∠B的度数.
如图,在△ABC中,∠A=60°,边BC的垂直平分线分别交AB,BC于点E,D,连接EC.若∠B=∠ACE,求∠B的度数. 如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.
如图,在△ABC中,∠C=150°,AC=4,tanB=$\frac{1}{8}$.