题目内容
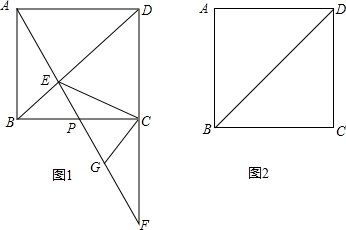
1.已知正方形ABCD的边长为3cm,点P从点B出发,沿折线BCD方向以1cm/秒的速度向终点D匀速运动,点P的运动时间为t秒,AP交BD于点E.(1)如图1,当点P在边BC上运动时,AP的延长线与DC的延长线交于点F,G是PF的中点.
求证:①△ABE≌△CBE
②∠ECG=90°
(2)如图2,探究:在点P的运动过程中,当t为何值时,△ECP为等腰三角形?请说明理由.
分析 (1)①由正方形的性质可知AB=BC,∠ABD=∠CBD,然后依据SAS证明△ABE≌△CBE即可;
②由正方形的性质可知:∠BCD=90°∠1=∠F,由全等三角形的性质可知∠1=∠2,于是得到∠F=∠2,由直角三角形斜边上中线的性质可知GC=GF,从而得到∠3=∠F,故此∠2=∠3 由∠2+∠4=∠3+∠4,可知∠ECG=∠PCF=90°;
(2)如图2所示,当点P在BC上时,由等腰三角形的性质可知∠5=∠2,由三角形的外角的性质可知∠6=2∠2,从而可知∠6=2∠1,于是可求得∠1=30,在△ABP中由勾股定理可求得t的值;当点P在CD边上时,如图3所示,先证明△ADE≌△CDE,从而得到∠DAE=∠DCE,由PE=PC可知:∠PEC=∠PCE由三角形外角的性质求求得∠APD=2∠DAP,从而得到∠DAP=30°,故此可求得DP=$\sqrt{3}$,于是可求得t=6-$\sqrt{3}$.
解答 解:(1)证明①∵ABCD是正方形,
∴AB=BC,∠ABD=∠CBD.
在△ABE和△CBE中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABD=∠CBD}\\{BE=BE}\end{array}\right.$,
∴△ABE≌△CBE.
②如图1所示: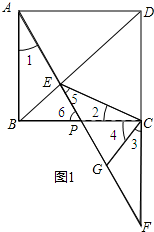
∵四边形ABCD是正方形.
∴∠BCD=90°∠1=∠F.
∵△ABE≌△CBE.
∴∠1=∠2
∴∠F=∠2.
∵在Rt△CFP中G是PF的中点,
∴GC=GF.
∴∠3=∠F.
∴∠2=∠3.
∴∠2+∠4=∠3+∠4,即∠ECG=∠PCF=90°.
(2)当点P在BC边上时,如图2所示: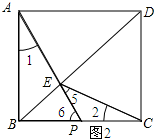
∵△ECP为等腰三角形,且∠EPC>90°,
∴PC=PE.
∴∠2=∠5.
∵∠6=∠5+∠2,
∴∠6=2∠2=2∠1.
∵∠1+∠6=90°,
∴3∠1=90°.
∴∠1=30°.
∴AP=2BP=2t.
在Rt△ABP中,32+t2=(2t)2,
解得:t=$\sqrt{3}$.
当点P在CD边上时如图3所示: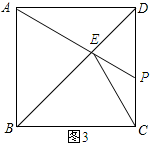
∵四边形ABCD是正方形,
∴AD=DC,∠ADE=∠CDE.
在△ADE和△CDE中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADE=∠CDE}\\{ED=ED}\end{array}\right.$,
∴△ADE≌△CDE.
∠DAE=∠DCE.
∵△ECP为等腰三角形,且∠EPC>90°,
∴∠PEC=∠PCE.
∵∠APD=∠DAE+∠DCE,
∴∠APD=2∠ECP.
∴∠APD=2∠DAP.
∴∠DAP=30°.
∴DP=AD×$\frac{\sqrt{3}}{3}$=3×$\frac{\sqrt{3}}{3}$=$\sqrt{3}$.
∵DP=6-t,
∴6-t=$\sqrt{3}$
t=6-$\sqrt{3}$.
综上所述,当t=$\sqrt{3}$,或t=6-$\sqrt{3}$时,△ECP为等腰三角形.
点评 本题主要考查的是四边形的综合应用,解答本题主要应用了正方形的性质、全等三角形的性质和判定、勾股定理、等腰三角形的性质,含30度直角三角形的性质,求得∠BAP=30°或∠DAP=30°是解题的关键.

 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案| A. | 3a-(2a-c)=3a-2a+c | B. | 3a+2(2b-3c)=3a+4b-3c | ||
| C. | 6a+(-2b+5)=6a+2b-5 | D. | (5x-3y)-(2x-y)=5x+3y-2x+y |
| A. | a3•a3=2a3 | B. | (a2)3=a5 | C. | a3÷a=a3 | D. | (-a2b)2=a4b2 |
| A. | sinA=$\frac{2\sqrt{2}}{3}$ | B. | cosB=2$\sqrt{2}$ | C. | tanA=$\frac{\sqrt{2}}{4}$ | D. | cosA=$\frac{1}{3}$ |
