题目内容
11.(1)计算(a2)3•(a2)4÷(a2)5(2)先化简再求值 (x+2)2-(x+2)(x-2),x=-3
(3)用简便方法计算:100$\frac{1}{2}$×99$\frac{1}{2}$
(4)已知:xm=3,xn=2,求x3m+2n的值.
分析 (1)先算乘方,再算乘除即可;
(2)先算乘法,再合并同类项,最后代入求出即可;
(3)先变形,再根据平方差公式进行计算即可;
(4)先根据同底数幂的乘法进行变形,再根据幂的乘方进行计算,最后代入求出即可.
解答 解:(1)(a2)3•(a2)4÷(a2)5
=a6•a8÷a10
=a4;
(2)(x+2)2-(x+2)(x-2)
=x2+4x+4-x2+4
=4x+8,
当x=-3时,原式=4×(-3)+8=-4;
(3)100$\frac{1}{2}$×99$\frac{1}{2}$
=(100+$\frac{1}{2}$)×(100-$\frac{1}{2}$)
=1002-($\frac{1}{2}$)2
=10000-$\frac{1}{4}$
=9999$\frac{3}{4}$;
(4)∵xm=3,xn=2,
∴x3m+2n
=x3m•x2n
=(xm)3•(xn)2
=33×22
=108.
点评 本题考查了整式的混合运算和求值,平方差公式,同底数幂的乘法,幂的乘方的应用,能运用所学的知识点进行计算是解此题的关键.

练习册系列答案
相关题目
1.某种袋装奶粉标明标准净含量为400g.抽检其中8袋,记录如下(“+”表示超出标准净含量,“-”表示不足标准净含量)
求:这8袋奶粉的总净含量是多少?
| 编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 差值/g | -4.5 | +5 | 0 | +5 | 0 | 0 | +2 | -5 |
6.下列说法中,错误的个数是( )
(1)两边与一角对应相等的两个三角形全等 (3)三个角对应相等的两个三角形全等
(2)两角和它们的夹边对应相等的两个三角形全等 (4)三边对应相等的两个三角形全等.
(1)两边与一角对应相等的两个三角形全等 (3)三个角对应相等的两个三角形全等
(2)两角和它们的夹边对应相等的两个三角形全等 (4)三边对应相等的两个三角形全等.
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
1.下列命题中是真命题的是( )
| A. | 全等三角形的对应边相等 | |
| B. | 两直线平行,同旁内角相等 | |
| C. | 两个角相等,这两个角一定是对顶角 | |
| D. | 相等的两个角是平行线所得的内错角 |
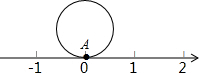 如图所示,把半径为1个长度单位的圆形纸片放在数轴上,圆形纸片上的A点对应原点,将圆形纸片沿着数轴无滑动的逆时针滚动一周,点A到达A′的位置,则点A′表示的数是-6.(π取3)
如图所示,把半径为1个长度单位的圆形纸片放在数轴上,圆形纸片上的A点对应原点,将圆形纸片沿着数轴无滑动的逆时针滚动一周,点A到达A′的位置,则点A′表示的数是-6.(π取3)