题目内容
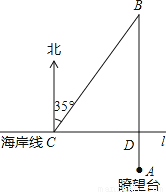
某海滨浴场东西走向的海岸线可以近似看作直线l(如图).救生员甲在A处的瞭望台上观察海面情况,发现其正北方向的B处有人发出求救信号,他立即沿AB方向径直前往救援,同时通知正在海岸线上巡逻的救生员乙.乙马上从C处入海,径直向B处游去.甲在乙入海10秒后赶到海岸线上的D处,再向B处游去.若CD=40米,B在C的北偏东35°方向,甲乙的游泳速度都是2米/秒.问谁先到达B处?请说明理由.
(参考数据:sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
 乙先到达B处。理由见解析
【解析】【解析】
由题意得∠BCD=55°,∠BDC=90°。
∵,∴BD=CD•tan∠BCD=40×tan55°≈57.2。
∵,∴。
∴。∴。
答:乙先到达B处。
在Rt△CDB中,利用三角函数即可求得BC,BD的长,则求得甲、乙的时间,比较二者之间的大小即可。
乙先到达B处。理由见解析
【解析】【解析】
由题意得∠BCD=55°,∠BDC=90°。
∵,∴BD=CD•tan∠BCD=40×tan55°≈57.2。
∵,∴。
∴。∴。
答:乙先到达B处。
在Rt△CDB中,利用三角函数即可求得BC,BD的长,则求得甲、乙的时间,比较二者之间的大小即可。
练习册系列答案
相关题目
若3x=4,9y=7,则3x-2y的值为( )
A.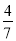 B.
B.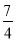 C.-3 D.
C.-3 D.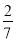
 A
【解析】
由3x=4,9y=7与3x-2y=3x÷32y=3x÷(32)y,代入即可求得答案.
A
【解析】
由3x=4,9y=7与3x-2y=3x÷32y=3x÷(32)y,代入即可求得答案. 两条直线相交,所成的四个角中,一定有一个是锐角。 (___)
 ×
【解析】试题分析:当两条直线互相垂直时,所形成的四个角都是直角,故本题答案为“×”.
×
【解析】试题分析:当两条直线互相垂直时,所形成的四个角都是直角,故本题答案为“×”. 函数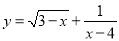 中.自变量x的取值范围是_____.
中.自变量x的取值范围是_____.
 x≤3
【解析】试题解析:根据题意得, 且x?4≠0,
解得.
故答案为:
x≤3
【解析】试题解析:根据题意得, 且x?4≠0,
解得.
故答案为: 在动画片《喜羊羊与灰太狼》中,有一次灰太狼追赶喜羊羊,在距羊村40m处追上了喜羊羊.如图中s表示它们与羊村的距离(单位:m),t表示时间(单位:s).根据相关信息判断,下列说法中错误的是( )
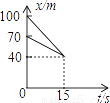
A. 喜羊羊与灰太狼最初的距离是30m B. 灰太狼用15s追上了喜羊羊
C. 灰太狼跑了60m追上了喜羊羊 D. 灰太狼追上喜羊羊时,喜羊羊跑了60m
 D
【解析】观察图象可得,喜羊羊与灰太狼最初的距离是100-70=30m,选项A正确;由横坐标看出,15秒灰太狼追上了喜羊羊,选项B正确;由纵坐标看出,灰太狼跑了100-40=60米追上喜羊羊,选项C正确;由纵坐标看出,灰太狼追上喜羊羊时喜羊羊跑了70-40=30米,选项D错误;故选D.
D
【解析】观察图象可得,喜羊羊与灰太狼最初的距离是100-70=30m,选项A正确;由横坐标看出,15秒灰太狼追上了喜羊羊,选项B正确;由纵坐标看出,灰太狼跑了100-40=60米追上喜羊羊,选项C正确;由纵坐标看出,灰太狼追上喜羊羊时喜羊羊跑了70-40=30米,选项D错误;故选D. 已知sinα=0.8536,则α=____度___分___秒.
 58 36 19
【解析】试题解析:由sinα=0.853 6,用科学计算器求得α≈58.605 4°,
所以α≈58度36分19秒,
故答案为:58;36;19.
故答案为:58;36;19.
58 36 19
【解析】试题解析:由sinα=0.853 6,用科学计算器求得α≈58.605 4°,
所以α≈58度36分19秒,
故答案为:58;36;19.
故答案为:58;36;19. 如果点A(-3,2m+1)关于原点对称的点在第四象限,求m的取值范围.
 m>-
【解析】试题分析:由于第四象限关于原点对称的点在第二象限,反之第二象限的点关于原点对称的点在第四象限,所以A(-3,2m+1)应在第二象限,由第二象限的符号特征解之.
∵A(-3,2m+1)关于原点对称的点在第四象限.
∴A(-3,2m+1)在第二象限.
∴A点的纵坐标2m+1>0.
∴m>-.
m>-
【解析】试题分析:由于第四象限关于原点对称的点在第二象限,反之第二象限的点关于原点对称的点在第四象限,所以A(-3,2m+1)应在第二象限,由第二象限的符号特征解之.
∵A(-3,2m+1)关于原点对称的点在第四象限.
∴A(-3,2m+1)在第二象限.
∴A点的纵坐标2m+1>0.
∴m>-. △ABC中,三个内角的度数均为整数,且∠A<∠B<∠C,4∠C=7∠A,求∠A的度数.
 44°
【解析】试题分析:先用∠A表示出∠C,再根据三角形的内角和等于180°列式整理用
∠A表示出∠B,再根据不等式求出∠A的取值范围,最后根据∠A是整数解答.
试题解析:
∵4∠C=7∠A,
∵∠A<∠B<∠C,
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍,
44°
【解析】试题分析:先用∠A表示出∠C,再根据三角形的内角和等于180°列式整理用
∠A表示出∠B,再根据不等式求出∠A的取值范围,最后根据∠A是整数解答.
试题解析:
∵4∠C=7∠A,
∵∠A<∠B<∠C,
由①得,
由②得,
∵∠A,∠C是整数,
∴∠A是4的整数倍, 下列分式是最简分式的是( )
A. 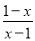 B.
B. 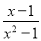
C. 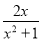 D.
D. 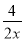
 C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C.
C
【解析】根据最简分式的特点,分子分母没有公因式,因此A可化为,不是最简分式;B可化为,不是最简分式;C是最简分式;D可化简为,不是最简分式.
故选:C. 
