Question

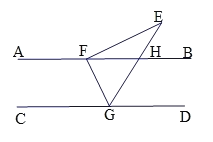
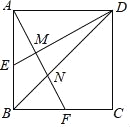
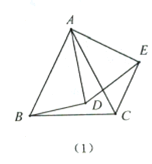
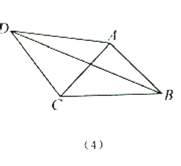
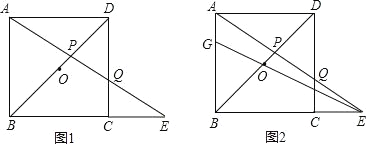
【题目】如图1，ABCD是边长为1的正方形，O是正方形的中心，Q是边CD上一个动点（点Q不与点C、D重合），直线AQ与BC的延长线交于点E，AE交BD于点P．设DQ=x．

（1）填空：当时，的值为　 　；

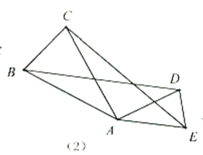
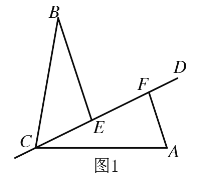
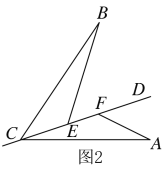
（2）如图2，直线EO交AB于点G，若BG=y，求y关于x之间的函数关系式；

（3）在第（2）小题的条件下，是否存在点Q，使得PG∥BC？若存在，求x的值；若不存在，说明理由．

Answer 1

【答案】（1）；（2）y=；（3）存在；x=；

【解析】

（1）先根据平行线分相等成比例定理得出==， =，然后根据已知条件求得CE=,进而求得QE=AE，AP=AE，后即可求得；

（2）过O作OM⊥AB，ON⊥BC，根据平行线分相等成比例定理得出CE=，进而求得BE=，然后根据=，即可求得解析式；

（3）根据PG∥BC求得==，根据对应边成比例得出y=，再根据（2）中求得的解析式解方程组，即可求得．

（1）

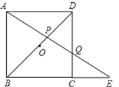
∵ABCD是边长为1的正方形，

∴AD∥BE，

∴==， =，

∵AD=BC=DC=1，DQ=，

∴QC=，

∴=，

∴CE=， =，

∴BE=，QE=AE，

∴=，即=，

∴AP=AE，

∴==；

（2）过O作OM⊥AB，ON⊥BC，

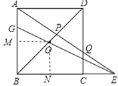
∵O是正方形的中心，

∴OM=MB=BN=ON=，

∵=，

∴=，

∴CE=，

∴BE=BC+EC=，

∵OM∥BE，

∴△GMO∽△GBE，

∴=，

即=，整理得：（2﹣x）y=1，

∴y=，

∴y关于x之间的函数关系式为y=；

（3）存在；

理由：∵PG∥BC，

∴==，

∵AG=1﹣y，GB=y，AD=1，BE=，

∴=，整理得：y=，

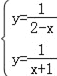解得x=，

所以当x=时，使得PG∥BC．